前言

前文说了Whitted-style光线追踪技术的原理以及光线与平面的交点计算方式，对于现在应用最广的Polygon Mesh显式曲面来说，一个复杂场景中的多边形面总数可能达到千万甚至亿万以上，如果每个光线都和场景中每个平面进行求交点计算，那么会进行像素数量 x 光线弹射次数 x 多边形平面数量次光线与平面交点计算。

例如下图中的经典场景，面数达到10.7M，渲染一张1080P图片，光线平均3次弹射，共需要进行66万亿次交点计算。

这样庞大的计算量是完全不能接受的，而显然一条光线在场景中弹射时和绝大多数平面是不会相交的，因此需要通过一些算法进行优化，这个算法就是今天要说的包围盒技术了。

 

轴对齐包围盒(Axis-Aligned Bounding Box)

用一个简单的方盒子称为包围盒（Bounding Box）完全包裹住物体，在光线与该物体的三角面计算求交之前先判断光线是否与包围盒相交，如果光线与包围盒没有交点的话，那么显然光线与盒内物体的所有三角面都不会有交点，自然也没有必要去遍历该物体的所有三角形面。

在几种包围盒方式中，AABB即轴对齐包围盒因为包围盒三组对面分别与与三个空间坐标轴平行，便于计算而使用最为广泛（下图中间）。

那么AABB包围盒就可以理解为三对平面的交集，这样可以方便进行光线与包围盒的求交运算。

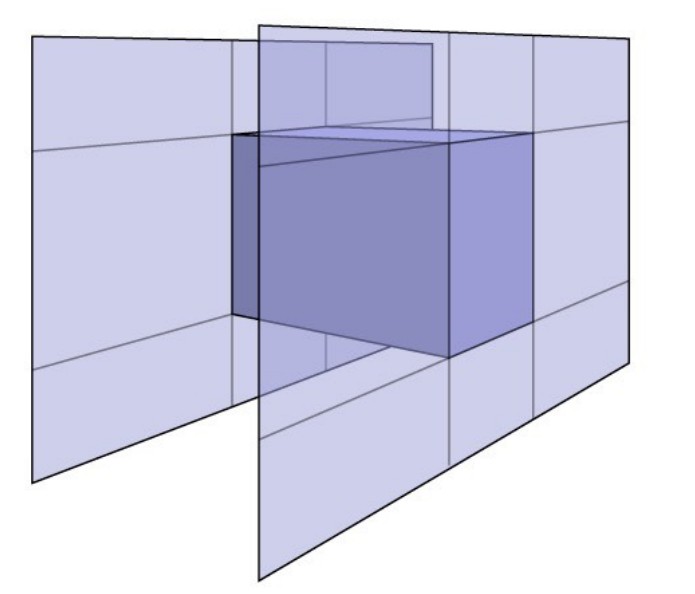
那么到底如何求光线与包围盒的交点呢？先将问题简化成直线与x0x1、y0y1两对平面的交点。

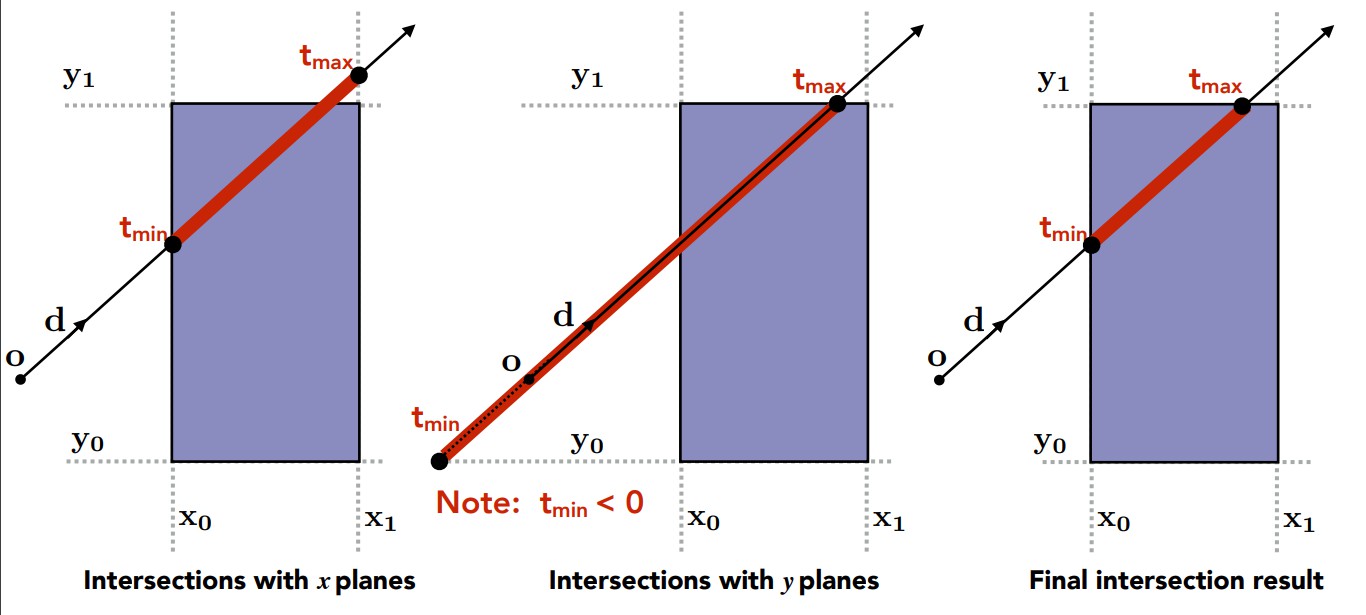
如上图最左边所示，求光线与一对x平面的交点，将先进入的交点(距离光线起点o最近的那个)记为 tmin, 后出去的交点记为 tmax，紧接着如中间图所示计算出光线与y平面的两个交点同样记为另外一组tmin, tmax，注意如果任意的 t < 0，那么这代表的是光线反向传播与对应平面的交点。

现在得到了光线与一对x平面的交点，与一对y平面的交点，究竟哪些点才是真正与盒子的交点呢？

1 只有当光线进入了所有的平面才算是真正进入了盒子中

2 只要当光线离开了任意平面就算是真正离开了盒子

所以对每对平面的tmin，tmax做如下运算(如果任意t值是负的也没有关系)

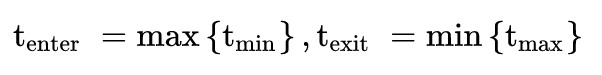
其中Tenter与 Texit分别对应了上述两点条件，而对应所举的2D例子，最终求出了两个真正的与包围盒的交点如最右边图所示（实际就是求两组交点构成的线段的交集——因为盒子是三组平面的交集）。

但光线不一定会与包围盒有交点，那么什么条件下才会有交点呢？

显然当Tenter < Texit的时候，光线所在直线一定在盒子中待过一段时间，也必然存在交点，但光线并不是直线，而是射线，除了保证了光线所在的直线在盒子里待过一段时间，还要考虑实际物理意义，具体如下：

• 如果Texit < 0，说明包围盒在光线后面，当然不会有交点
• 如果Texit >= 0 并且 Tenter < 0，说明光线是从包围盒内发射出来的，显然有一个交点
• 如果Texit >= 0 并且 Tenter >= 0，说明包围盒在光线前面，有两个交点

因此，只要满足Tenter < Texit并且 Texit >= 0 ，光线就一定和包围盒有交点。

根据前文中光线与平面的交点算法，光线和包围盒的求交也很容易写出如下：

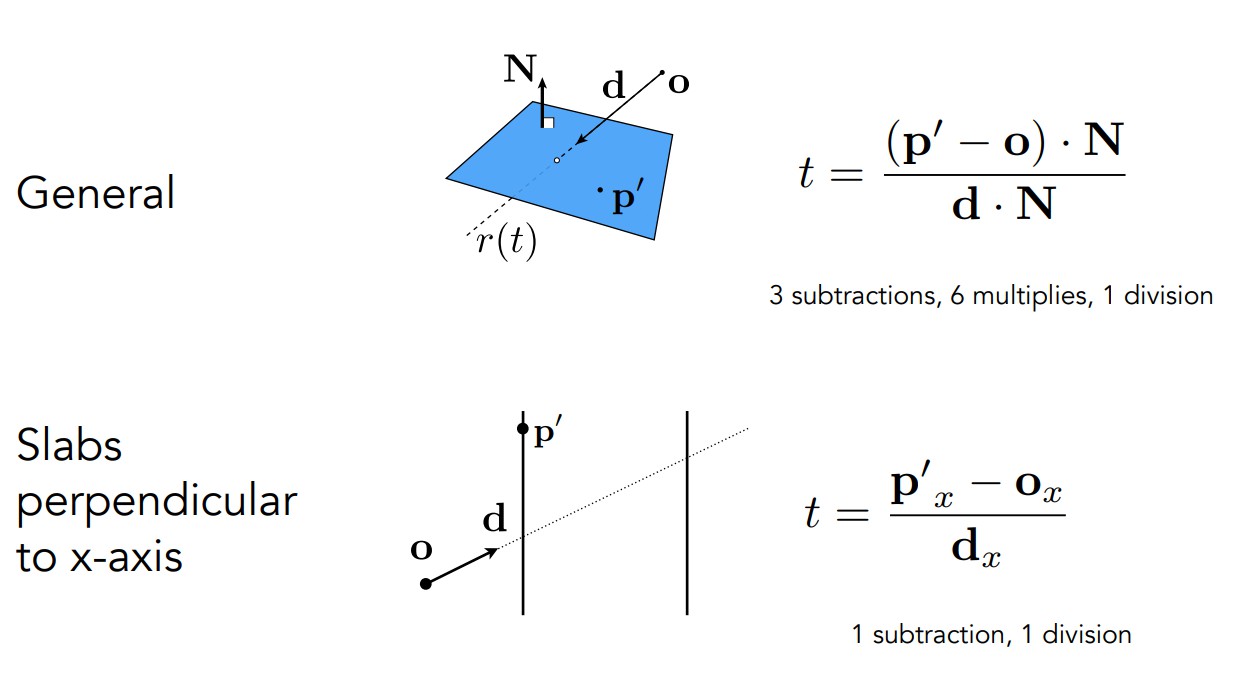
以一对x轴的平面为例，两个平面肯定垂直于x轴，因此可以直接求光线在x轴方向的分量，代入公式从而直接得到t值，计算过程比光线与任意平面交点的算法要快速得多，这也是AABB包围盒得到广泛使用的原因。

 

AABB划分方法

虽然对场景中的每个物体使用AABB包围盒技术已经可以大幅加快光线追踪效率，实际使用中难免遇到以下两种极端情况：

• 整个场景主要只有一个极其复杂的单一人物模型，那么只对这一个物体做包围盒的话，相当于对效率没有提升
• 整个场景充斥着大量的细小模型，如植物、建筑之类的，每个模型可能只有很少的面，如果此时对每个物体求包围盒，得到的包围盒数量会非常多，效率提升有限

基于以上两点考虑，AABB不应只局限于以物体模型为单位，可以更加精细的划分成以一定数量的三角面为单位，并且对于场景的许许多多包围盒来说应该要有一种数据结构将其统一起来。

因此为了更好地划分场景形成不同的AABB，使得划分之后的AABB能够更好的加速光线追踪，在AABB的基础上出现了多种划分方法。

 

均匀空间划分Uniform Spatial Partitions

先从最简单的划分方法，均匀空间划分（也称为Grid划分）开始介绍。

第一步，将整个场景包裹在一个大的包围盒中：

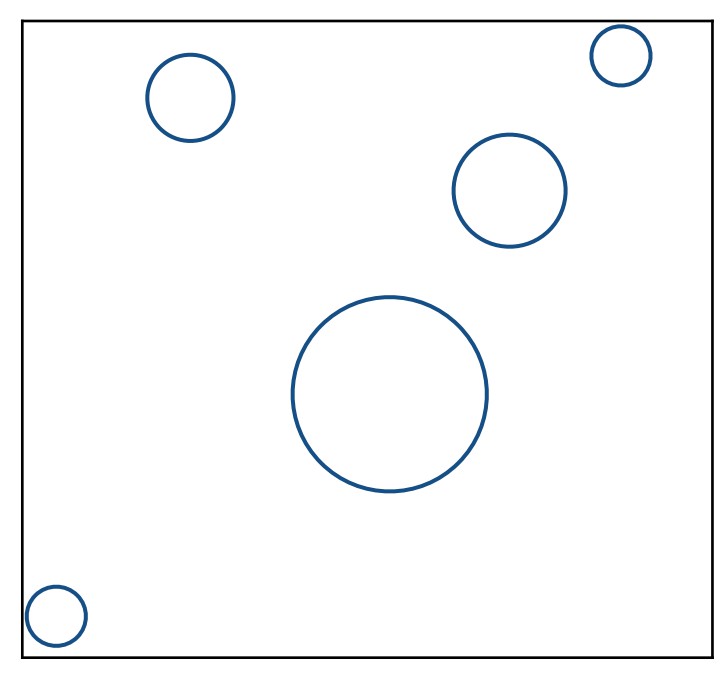
第二步，均匀划分这个大包围盒，变成很多小方格：

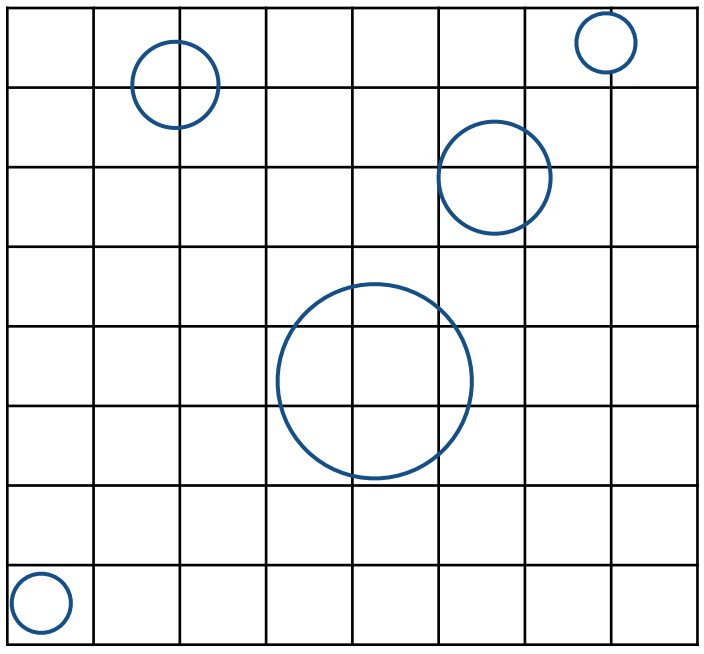
第三步，在每个小方格上存储物体模型信息

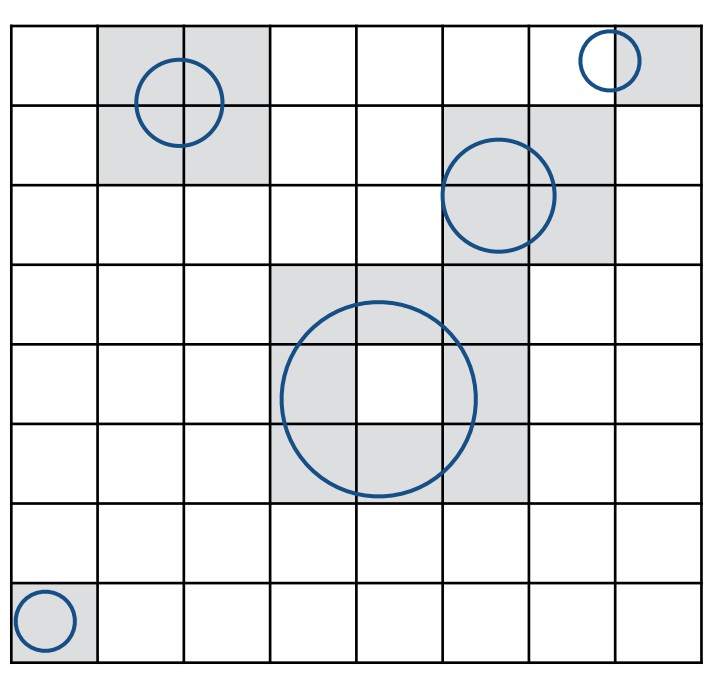
在光线追踪计算时，根据光线的方向找到所有相交的小方格，倘若小方格中存储有物体，再进一步与方格中的物体模型或是三角形面求交。

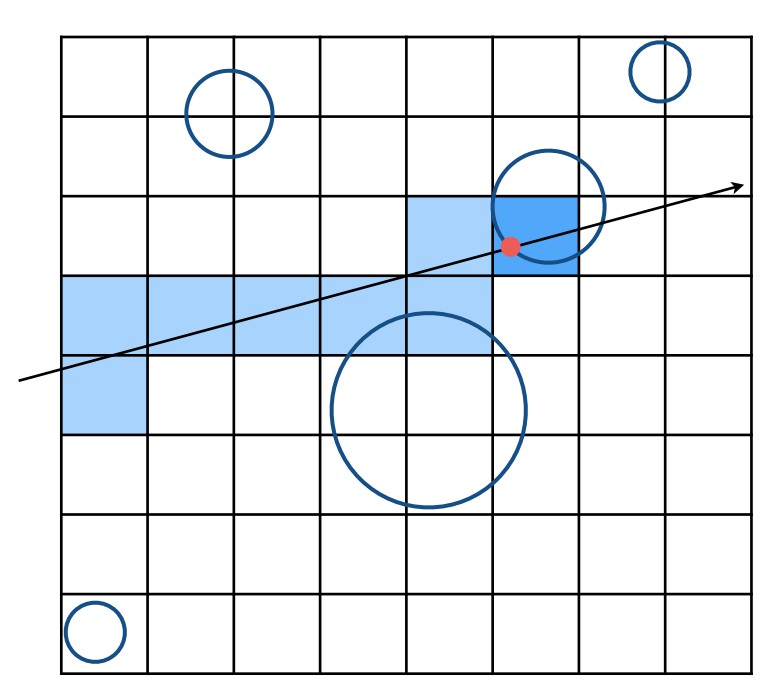
以上就是均匀空间划分的全部过程了，简单来说就是将空间划分为多个均匀的小的AABB，再根据光线方向找出相交的小方格(这一步并不需要判断所有方格，可以用类似brenham的方法来做)，再判断小包围盒中是否存储了模型信息，若有则进一步求交。

但这种划分方法假设了找出相交方格要比直接判断与物体求交相对容易，因此划分方格数的数量也是影响性能的关键，方格太少就没有加速效果，方格太多则判断与方格的求交可能会拖累效率。

因此这种方法最适合的场景就是空间中均匀布满了三角形面，如下图这种场景：

如果场景较为空旷，物体较小且相互距离较远，那么均匀分割的效果就会很差了，因为会有很多无效的方格与光线的求交过程。

 

KD-Tree空间划分

KD-Tree属于树形划分，类似的还有Oct-Tree以及BSP-Tree等划分方法。

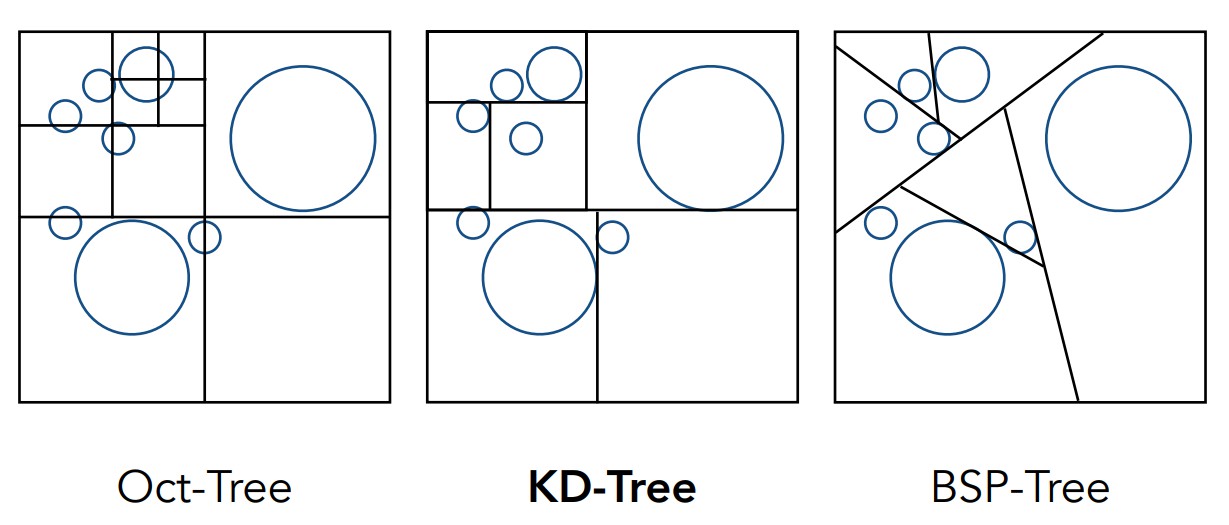
第一种Oct-Tree，也就是八叉树，每次将空间分为8个相等的部分（三维空间横竖平各切一刀，因为图中是二维显示，所以看起来只划分了4部分），再递归的对子空间进行划分。当划分的子空间足够小或是空间中三角形面的数量很少的时候会停止划分。这种方法的显著缺点是，随着维度的上升划分的空间数量会呈指数级增长。

第二种KD-Tree，也是下面将详细介绍的方法，其每次将空间划分为两部分，且划分依次沿着x-axis，y-axis，z-axis，即如图中所示，第一次横着将2维空间分为上下，第二次再竖着将上下两个子空间分别划分为左右部分，依次递归划分，划分时不是按空间大小而是按模型数量或者三角形数量进行均匀划分，终止条件与八叉树类似。

第三种BSP-Tree，其与KD-Tree类似，唯一不同的是划分不再沿着固定一轴，可以任意方向划分，缺点自然是划分的空间没有规则性，求交比较困难。

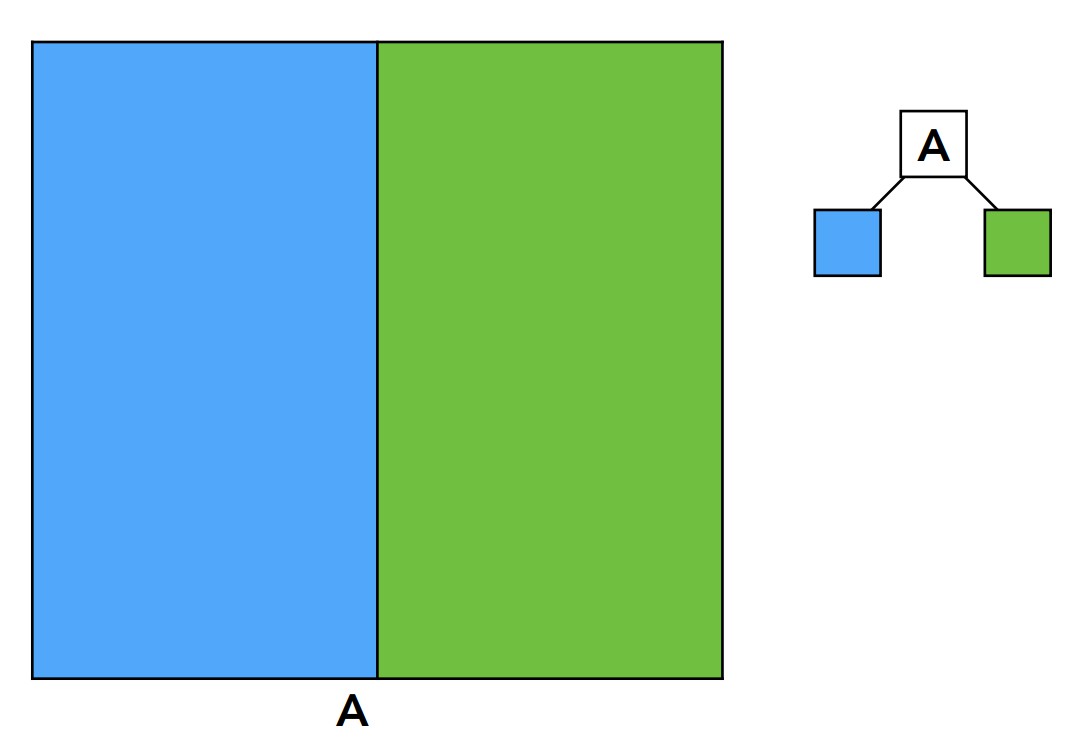
接下来从一个例子具体介绍KD-Tree，第一步将空间分为两部分。

第二步对左右两个子空间换个方向再分为两部分(这里为方便展示，只画出了右半部分，其实左边也是一样)

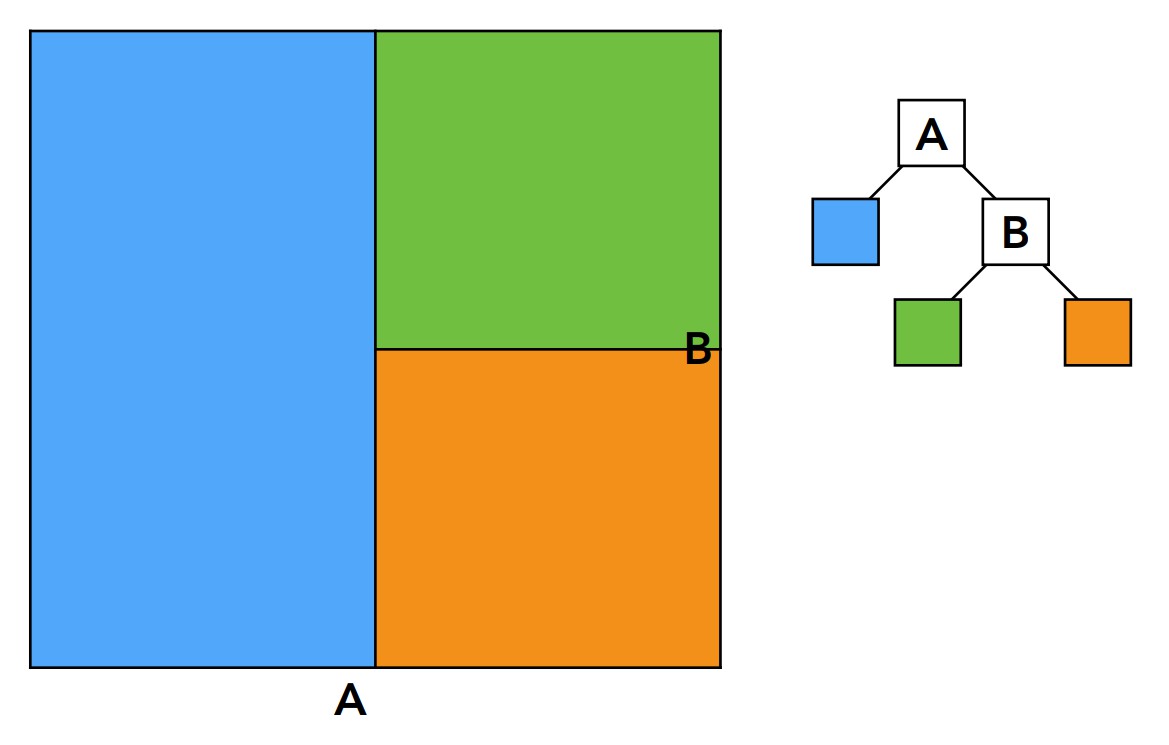
如此递归的划分下去，且在划分过程当中遵循这样几点：

1 依次沿着x-axis,y-axis,z-axis划分，使得空间被划分的更加平衡

2 划分的位置由空间中三角面的分布决定，具体细节不展开

3 叶子节点存储对应空间的所有物体或三角面信息，中间节点仅存储指针指向两个子空间

4 当划分空间太小或是子空间内只有少量三角形则停止划分

当KD-Tree建立完成之后，如何进行光线与物体求交判断呢？

第一步，判断光线是否与最外层的包围盒相交

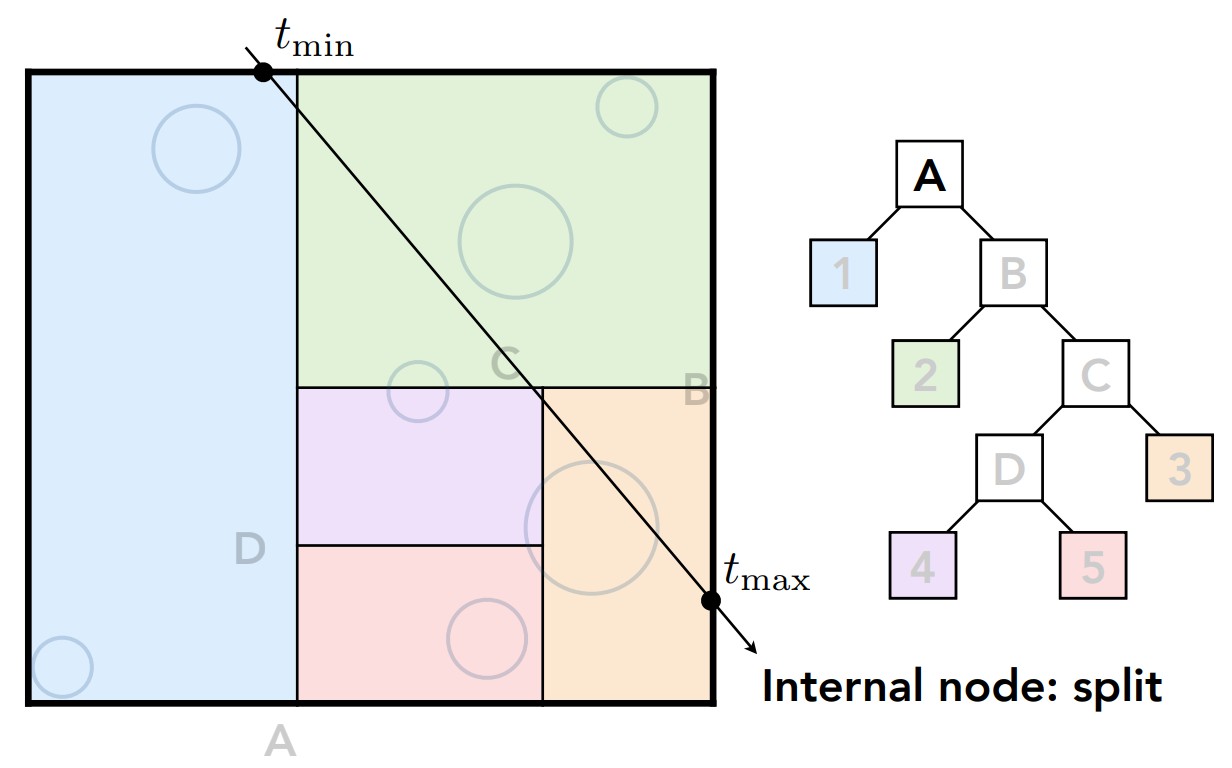
如果相交进一步判断是否与对应的两个子空间相交

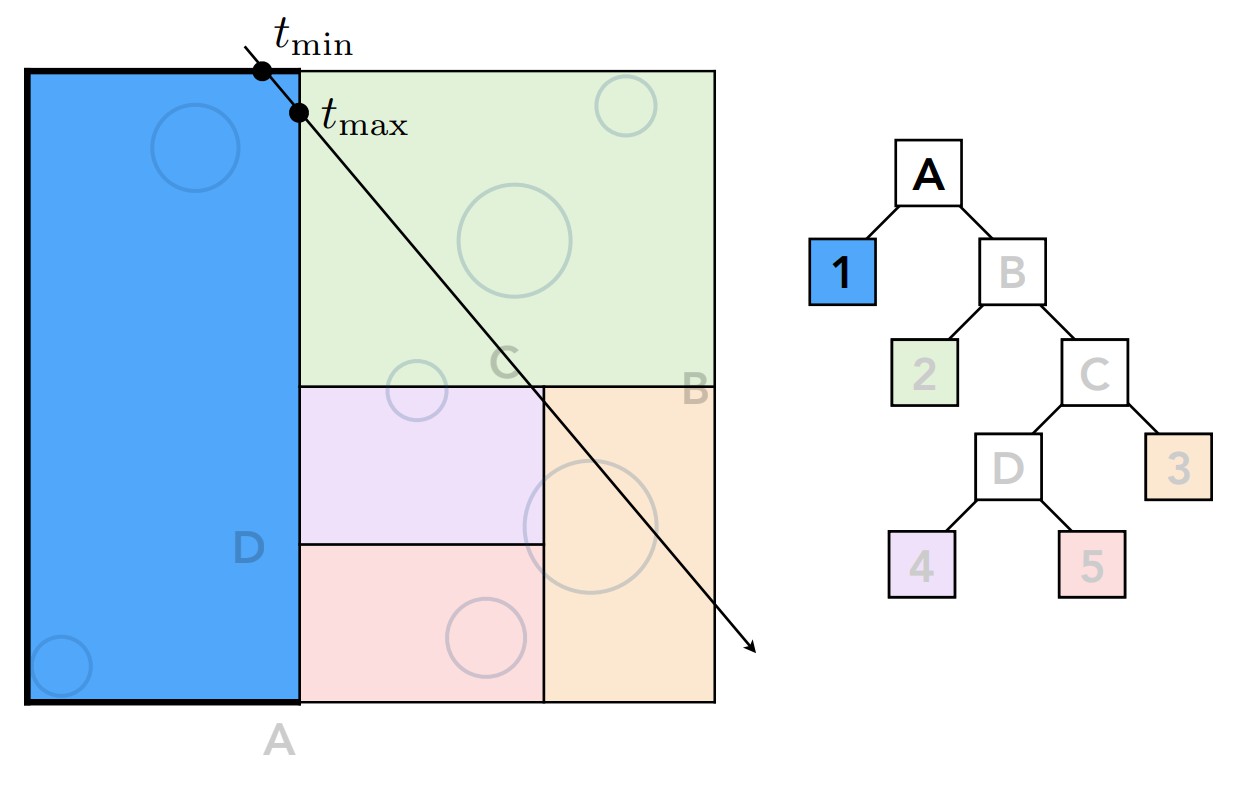
上图是为了显示方便，所以左侧没有进行进一步的显示划分情况，实际会继续划分下去的，所以左半部分对应的1号空间是叶子节点，如果光线与之相交，进一步判断与存储与叶子节点的物体信息求交。左半边判断完之后，接着判断右半部分，显然光线与左右两侧包围盒都相交。

则对于左右两侧的所有子包围盒，递归的执行这个步骤即可。

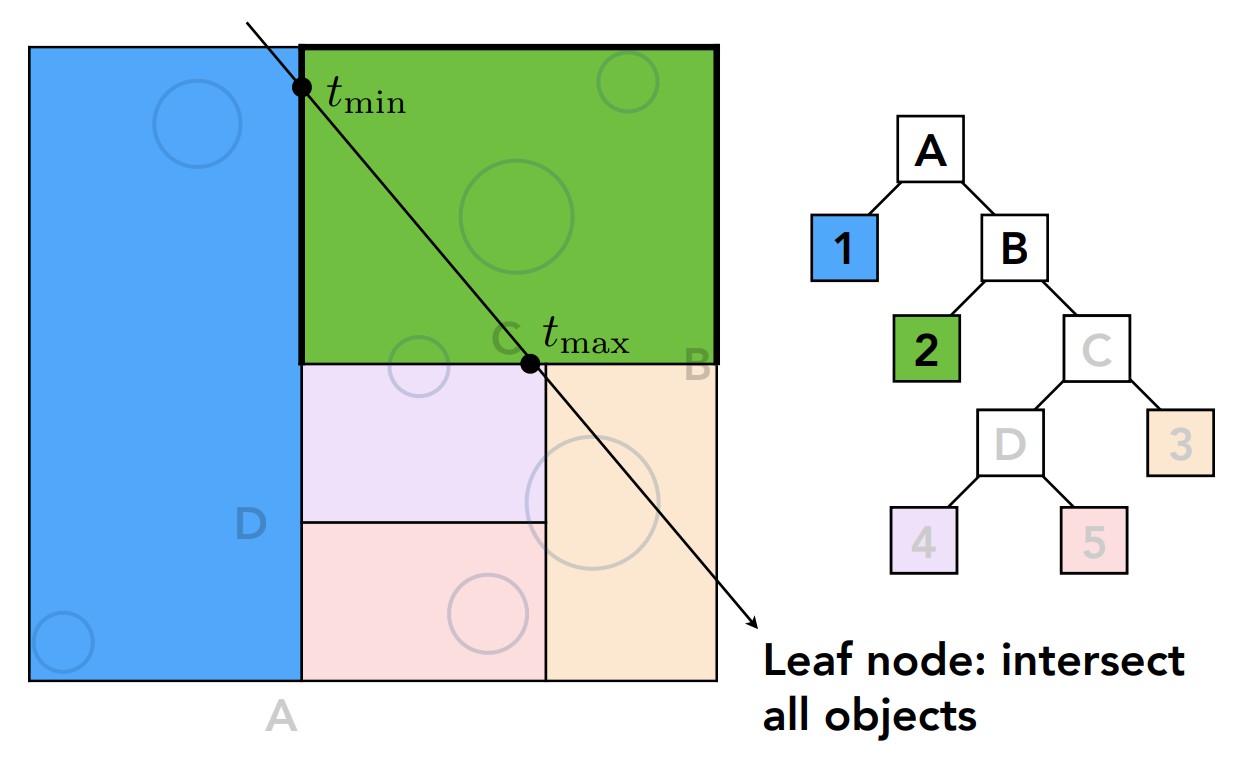
更加详细的过程就不再赘述。

优点： 利用KD-Tree的结构来构建AABB的好处是倘若光线与哪一部分空间不相交，那么则可以省略该部分空间所有子空间的判断过程，在原始的纯粹的AABB之上更进一步提升了加速效率。

缺点： 判断包围盒与三角面的是否相交较难，因此划分的过程不是那么想象的简单，其次同一个三角面可能被不同的包围盒同时占有，这两个不同包围盒内的叶节点会同时存储这一个三角形面

上面详细介绍了利用AABB的均匀划分方法，KD-Tree划分方法，也简略提及了Oct-Tree以及BSP-Tree。但其实这些技术在业界之中已经逐渐不再被广泛使用，但依然有很多借鉴参考价值。

下面会介绍一种现在被广泛使用的加速光线追踪的方法，即Bounding Volume Hierarchy。

 

BVH对象划分(Bounding Volume Hierarchy Object Partitions)

BVH（Bounding Volume Hierarchy）与前几种方法最显著的区别就是，不再以空间作为划分依据，而是从对象的角度考虑，即三角形面，过程如下： 第一步同样找出场景的整体包围盒作为根节点

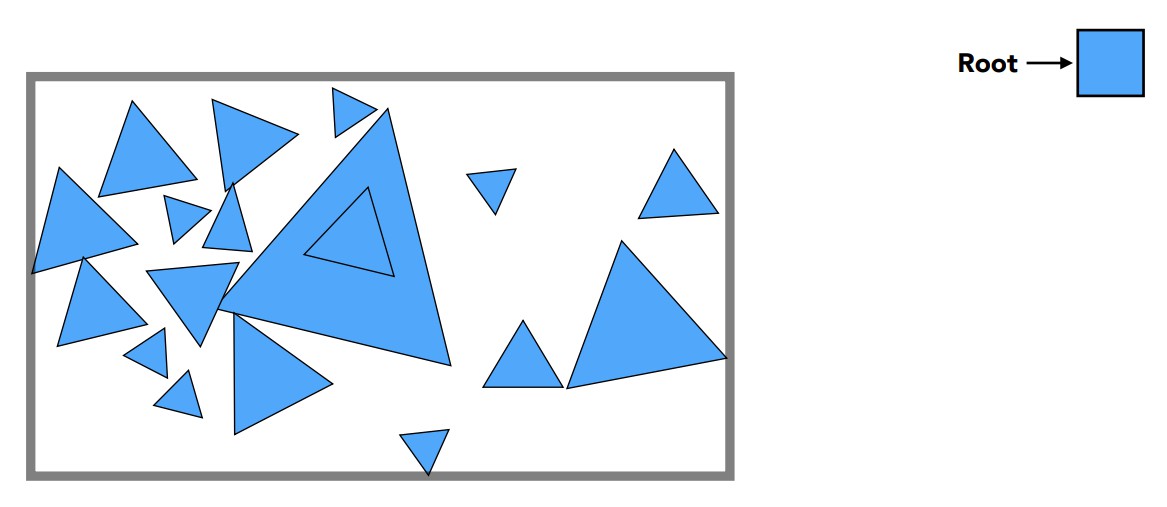
第二步找到合适的划分点，将最大包围盒内的三角形面分为两部分，再分别重新计算新的包围盒

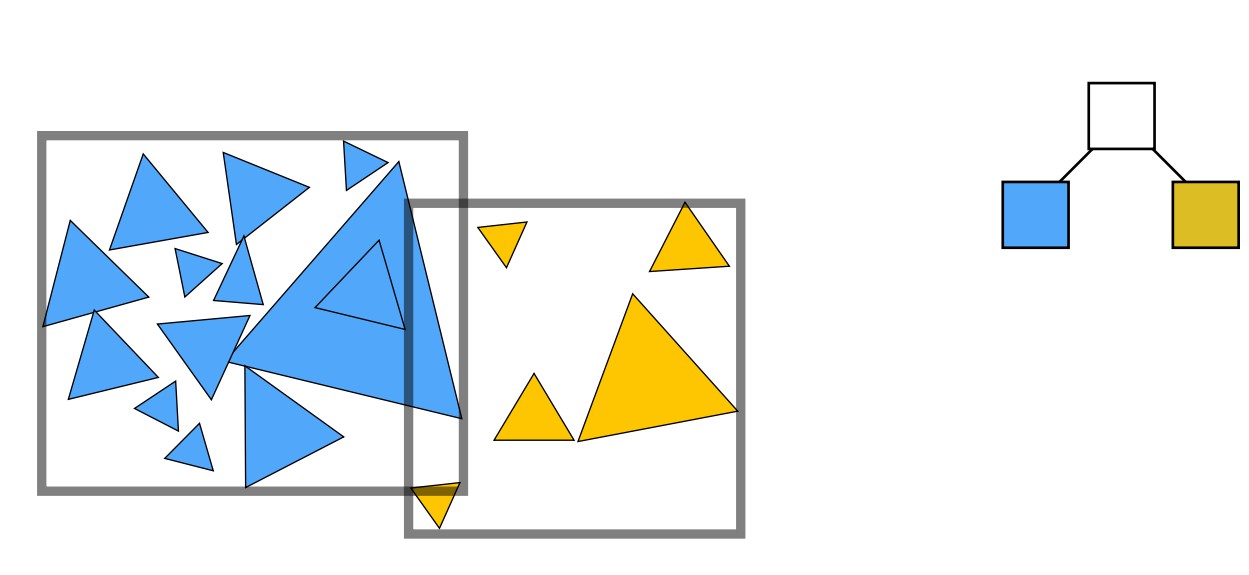
注意包围盒会重叠，但一个三角形面只会被存储在唯一的包围盒内，而这也就解决了KD-Tree的缺点。接下来与KD-Tree的建立类似，递归的对所有子空间重复该步骤。

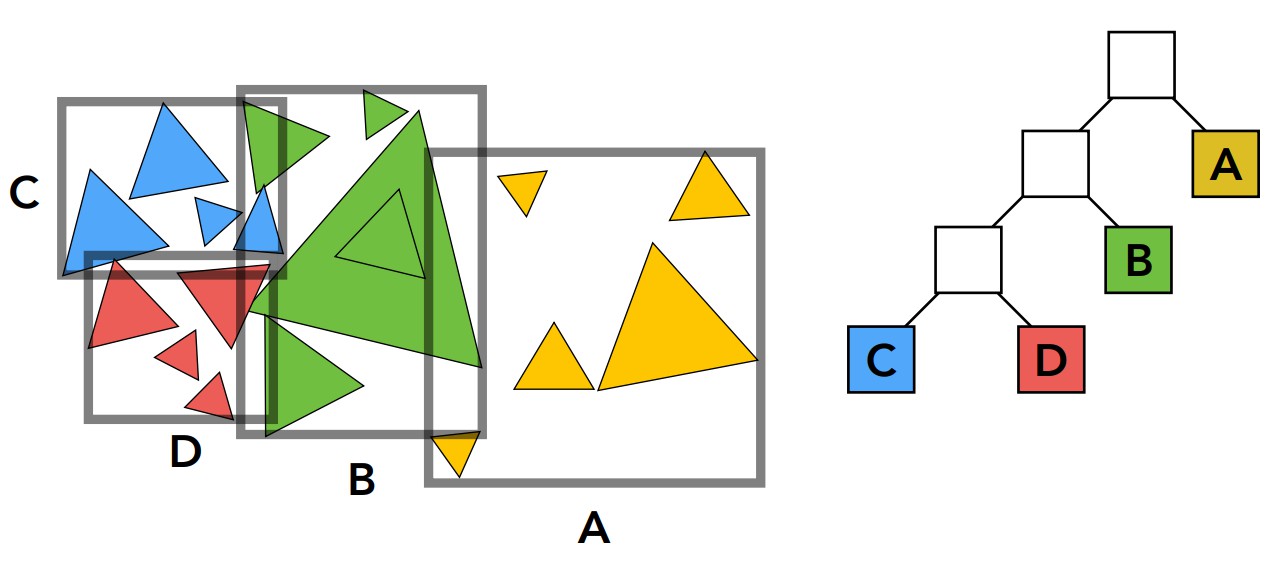
最终可以建立出如上图的所示的树形结构，同样为了画图方便，只进行了左半部分的划分，右半部分其实同理。

每次划分一般选择最长的那一轴划分，假设是x轴，那么划分点选择所有三角面的重心坐标在x坐标上的中位数进行划分，如此便能保证划分的三角形左右两边三角形数量尽可能差不多，当然也就使得树形结构建立的更加平衡，深度更小，平均搜索次数更少，提高效率。

而与KD-Tree一样，中间节点不存储物体三角面信息，只在叶节点中存储，终止条件为当前包围盒内三角形数量足够少（例如5个）。

 

本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记，感谢。

---

当我们凶狠地对待这个世界时，
这个世界突然变得温文尔雅了。

——余华