前言

之前在光照模型基础之Lambert一文中简单介绍了向量的点乘，今天就详细介绍一下向量的点乘和叉乘的概念以及在计算机图形学中的应用。

向量

在说点乘与叉乘之前先复习一下向量，或者说矢量。

向量是由方向和大小构成的，可以形象化地表示为带箭头的线段，箭头代表方向，线段长度代表向量的大小。

向量没有固定的起点，只要方向相同，大小相等，就认为两向量是相同的。

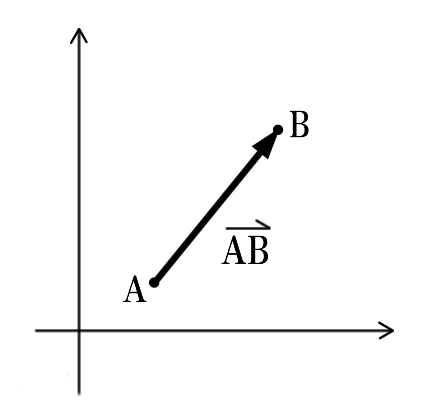
对于由起点A指向终点B的向量，向量AB可以表示为终点坐标-起点坐标，即向量AB = B – A，而为了表示方便，将起始点放到原点，就可以用此时点B的坐标表示该向量。

向量的大小

向量的大小，也就是向量的长度(或称模)，向量a的模记作|a|，它是一个非负实数。

因为方向不能比较大小，因此两个向量不能直接比较，只能比较长度的大小。

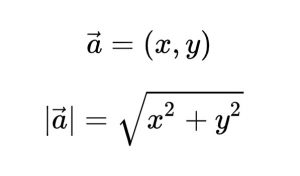
在数学中，向量的不同坐标一般写作横向的单行形式，而在计算机图形学中，为方便进行矩阵计算，向量一般写作纵向的单列形式，称为列向量。

长度为一个单位（即模为1）的向量，叫做单位向量，显而易见，用向量除以自身的长度即可得到自己方向上的单位向量。

长度为0的向量，叫做零向量，零向量的起点和终点重合，所以零向量没有确定的方向，或说零向量的方向是任意的，不能说零向量没有方向。

向量的加减乘除

两个向量的加减法满足平行四边形定律。

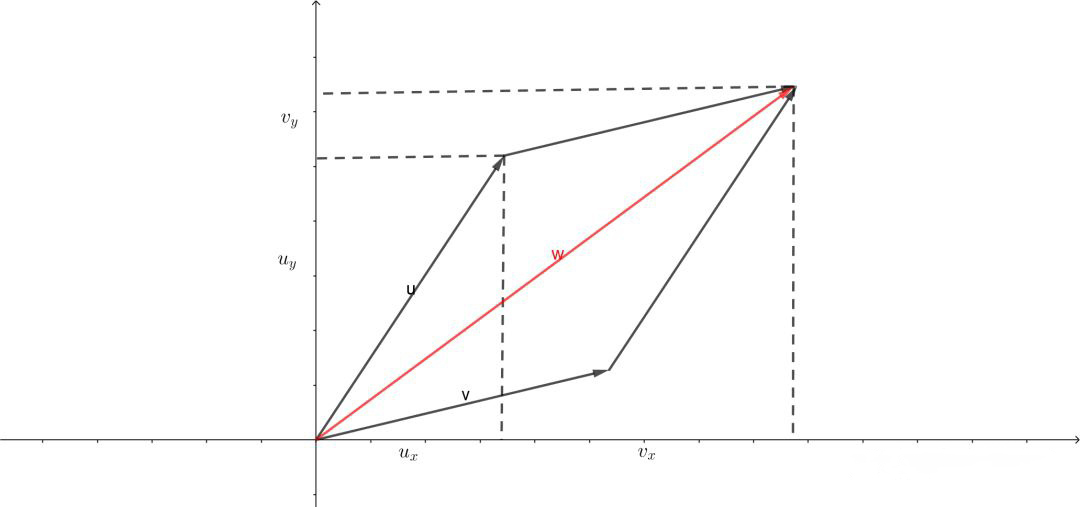
计算方式则是对应坐标的加减。

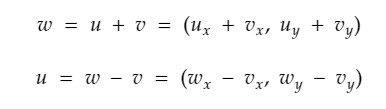
而向量与数的乘除运算则是坐标与数的分别相乘，可以理解为向量的缩放，长度改变而方向不变。

点乘

点乘又名点积，英文为DotProduct，是两向量之间的一种运算方式，计算方式是对应坐标的乘积之和，结果为一个标量，它的几何意义是A向量在B向量上的投影的长度乘以B向量长度，两向量夹角小于90度时点乘大于0，夹角大于90度时点乘小于0，刚好90度时点乘为0。

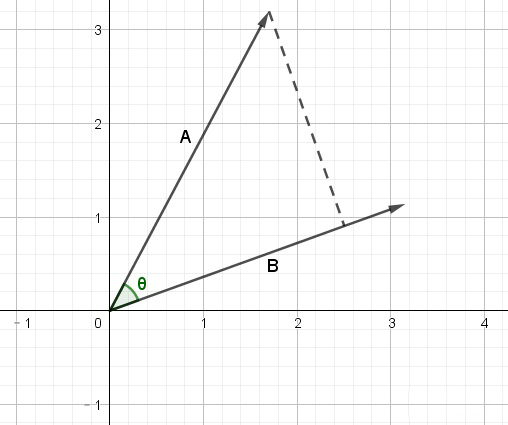
计算方式为如下

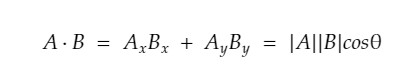
稍一变形就可以得到求两个向量夹角的方式

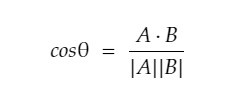
那么对于单位向量c和d来说，因为长度为1，因此cosθ = c · d。

点乘满足交换律、结合律以及分配律。

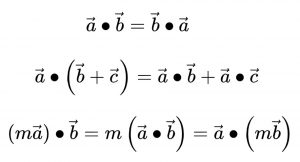
通过点乘，就可以用来判断两个向量的夹角关系，比如是否垂直、平行、同向、逆向，相似度大小（点乘越大，夹角越小，相似度越高）；或者用于空间变换，将向量投影到特定空间。

还可以用来将向量分解为两个垂直方向的分量，如下

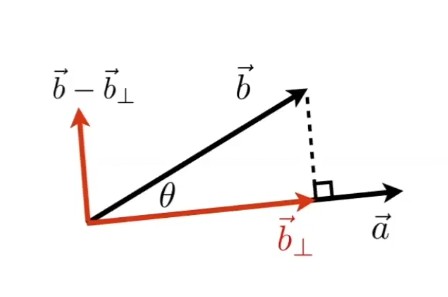
叉乘

叉乘又名叉积，英文为CrossProduct，是两向量之间的一种运算方式，它的几何意义是根据A、B两个向量，生成第三个向量C，C的方向垂直于A、B所构成的平面，大小则是A、B两个向量构成的平行四边形的面积。

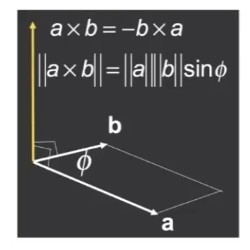
C的垂直方向满足于右手螺旋定则，axb即右手四指从a的方向向b的方向握拳，此时大拇指伸直的方向就是axb的方向。

而当bxa时，右手拇指会指向axb的相反方向，因此叉乘不满足交换律，而是满足反交换律。

叉乘的计算方式如下

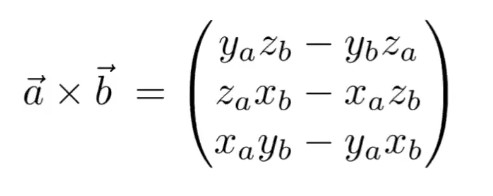
因此，基于叉乘，可以在三维空间中创建直角坐标系，当从x轴叉乘y轴时得到的是z轴时，该直角坐标系就被称为右手直角坐标系，这也是大多数图形API的坐标系；而从x轴叉乘y轴时得到的是-z轴时，该直角坐标系就被称为左手直角坐标系。

除了反交换律外，叉乘还满足结合律与分配率，并且向量与自身的叉乘是零向量。

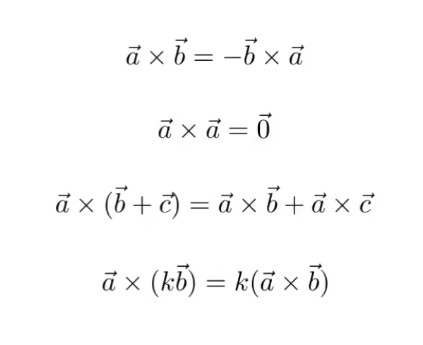
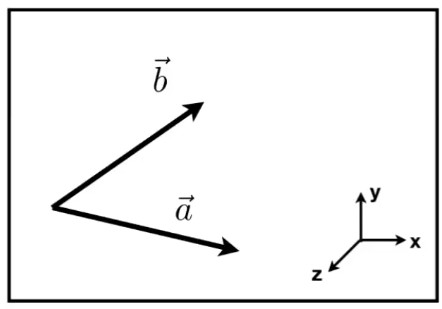
在计算机图形学中，通过叉乘可以用来判断两个向量的左右关系，当a x b得到的z向量是正值时，说明b向量在a向量的左侧；而当a x b得到的z向量是负值时，说明b向量在a向量的右侧。

而同样基于左右的判断，就可以得到点对于三角形来说的内外关系，当ABxAP、BCxBP、CAxCP判断出P点在三个向量的左侧时，P点就位于三角形ABC之内；而反向取CBxCP、BAxBP、ACxAP判断出P点在三个矢量的右侧时，P点也位于三角形ABC之内。

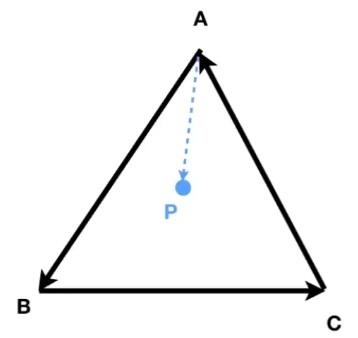
因此只要对三角形按时针循环方向取向量，无论正逆，只要得到的P点都在三个矢量左侧或者都在三个矢量右侧，则P点必定位于三角形之内；反之则在三角形之外。

这个方法被广泛用于GPU渲染流程的光栅化阶段等处。

本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》系列教程，感谢。

在我们生活的这个世界上，
最大的不幸就是有些人完全拒绝新奇。

《思维的乐趣》
——王小波