前言

纹理贴图不只可以用来给模型指定颜色，也可以用来设置金属度、粗糙度、反射度、光泽度等数值类属性，还可以用来为模型添加表面细节效果。

 

Normal Map（法线贴图）

在Blinn-Phong光照模型中，法线向量是其中极为重要的角色，不同的法线向量对光照的计算结果有着巨大的影响，例如下图将一个高精度模型的法线信息套用在低精度模型之上，会使低精度模型的渲染效果有着巨大的提升。

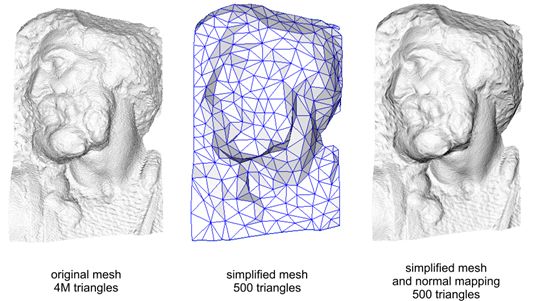
像上面这样用低精度的模型进行渲染就可以得到逼近高精度模型的效果，既大大节省了模型存储所需的空间，也可以降低对硬件的性能要求。

那么问题来了，如何将高精度模型的法线信息保存下来呢？

前文说过贴图上可以存储三维的颜色信息作为漫反射颜色，自然也可以存储其他类型的信息，法线向量这种三维信息也不例外。

只要将高精度模型的法线信息存储在贴图上，在低精度模型渲染时利用UV坐标去查询每个点在贴图上对应的法线信息，代替模型的原来法线信息进行着色计算，就可以实现这样的效果，而这种贴图就叫做Normal Map法线贴图。

那么具体怎么在贴图上存储法线信息呢？

一种可选的方法是，存储object space下的法线向量坐标(这会使得法线贴图看起来五颜六色的)，好处是取出来转换到世界坐标就可以直接使用，坏处是无法镜像任何UV，在对称模型上会浪费大量纹理空间，且不支持UV动画或者模型变形动画。

这也就引出了第二种方法，存储切线空间的法线向量坐标(这会使得法线贴图大部分呈蓝色)，其中，B通道表示法线方向的斜率；R通道表示左右切线方向的斜率；G通道表示切线方向向上或向下的斜率（OpenGl向上，DirectX向下）。下面会仔细介绍这种方法。

任何空间坐标系都要由3个互相正交的基底向量构成，切线空间也不例外，如下图所示：

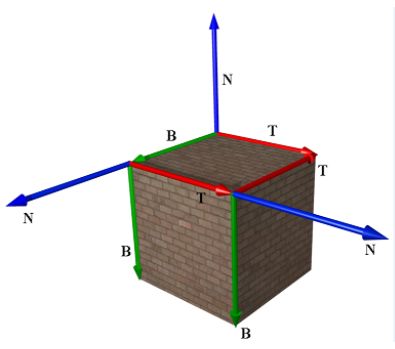
其z轴由原来该面上的几何法线n构成，指向物体表面的外侧。x，y轴分别由该面所对应的贴图上的U,V两个方向构成，称之为tangant轴和bitangent轴。

我们称tangant轴（t）、bitangent轴（b）及法线轴（N）所组成的坐标系，即切线空间（tbn）。

法线向量N可以根据原来的模型信息得到，如何去计算t和b呢？

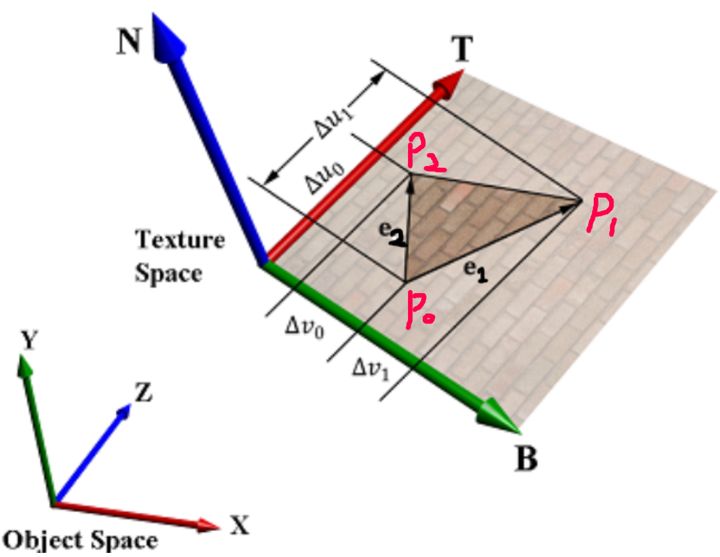
如上图所示，记一个三角形的面的三个顶点分别为p0,p1,p2，并且使用(ui,vi)来表示对应顶点的texture坐标，那么根据顶点坐标的差值，纹理坐标的差值，以及t,b两轴，可以得到如下关系：

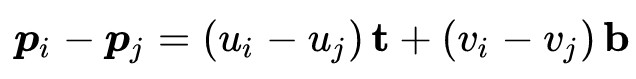
为了进一步简化公式，设：

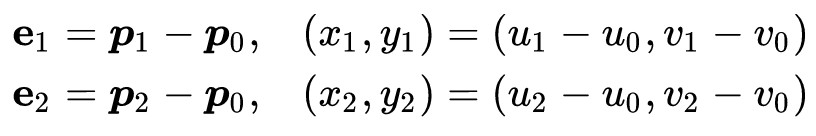
那么便可以把第一个公式简化为如下形式：

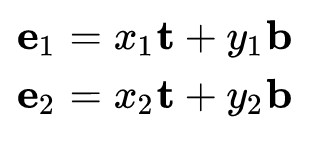
利用线代知识，将其写为矩阵形式:

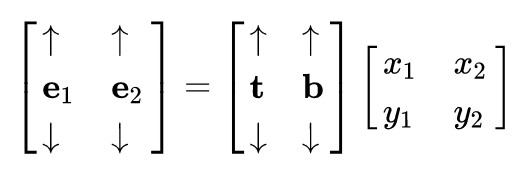
两边同乘系数矩阵的逆即可得到:

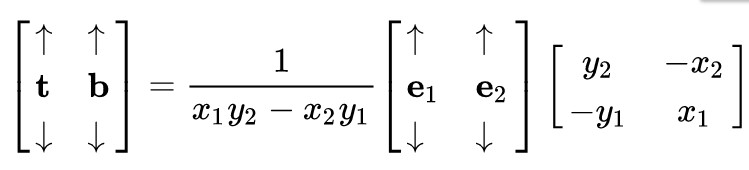
其中右边式子中的变量全部已知，自然就已经成功求出t,b两轴向量，再加上原几何法线向量n，至此便已经得出了切线空间(tbn)。法线贴图的数据就存储在空间之下，对于没有变动的法线向量就是(0,0,1)而这恰巧也就解释了为什么法线贴图大部分都是蓝色的(因为大部分法线一般不变动)。

具体实施的时候只需利用[t b n]向量组成的矩阵乘以法线贴图上的存储3维信息，即可得到正确的法线向量了，此时正确法线向量所存在的坐标系与用在构建该坐标系的法向n是同一个坐标系下(当然也就是记录p0,p1,p2的坐标系)。

需要注意的是求出来的t,b两轴并不一定保证垂直，有时候还需再加一步施密特正交化如下：(提一句施密特正交化的几何意义就是减去除了与之垂直的所有分量值，剩下的就只有垂直分量了)

另外真正存储的时候只需要t 和 n即可，第三轴可以直接叉乘得到。并且将t和n作为顶点的属性进行存储，正如顶点n是共享该点的面法线均值，t同样是所有共享该点的三角面分别计算出来t的均值，与法线可以作为定点属性插值一样，t也可以进行插值计算。

 

Bump Map（凹凸贴图）

Bump Map其实与Normal Map十分类似，Normal Map直接存储了法线信息，而Bump Map存储的是该点逻辑上的相对高度(可为负值)，该高度的变化实际上表现了物体表面凹凸不平的特质，利用该高度信息，再计算出该点法线向量，最后再利用该法线计算光照，这就是Bump Map的过程，只不过比直接的Normal Map多了一步从height到normal向量的计算。

因为Bump Map影响的是物体表面的相对高度，因此有时也称作Height Map（高度贴图）。

Bump Map上颜色越浅代表该位置的表面越向外凸起，颜色越深代表该位置的表面越向内凹陷，因此Bump Map相比Normal Map能够更加直观地预览表面凹凸的效果。

那么所需要关心的问题就是，如何从相对高度计算出法线向量呢？

假设上图中黑色的线是原本一个比较光滑的面，在这里应用了一个Bump Map决定相对高度如何变化，得到了黄色的线，那么原来点的位置会被认为因Bump Map而改变，那么法线也会改变。

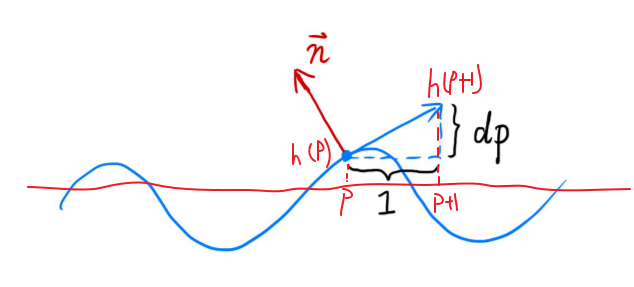
先简化一下问题，在一维空间下来计算，点p原来的法线n为(0, 1) ，我们要求出改变后的法线，可以先求出与法线垂直的切线，设切向量为（x，y），点p被改变后的高度记为h（p）。

利用微分的思想，找相邻像素点的位置即p+1处，也有一个高度h（p+1），通过这两点的高度差，就可以算出切向量的y值，即为dp，x的值就是相邻两个像素的x差值1，因此切向量即为（1，dp），根据逆时针旋转90度的旋转矩阵可以得到法向量为（-dp，1），即法线为（-dp，1），最后归一化为单位向量。

将刚刚一维上一条线的思维推广到二维上uv平面内的操作，对于u和v两个维度我们就可以得出下面的公式。

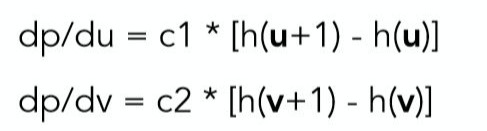
最后可以得到法线为(-dp/du, -dp/dv, 1)，最后归一化为单位向量即可。

注意，所有计算出来的法线都是局部坐标即切线空间之下，因此还需要左乘[t b n]矩阵转到(世界)相机坐标系之下得到正确法线方向。

 

Displacement Map（置换贴图）

Displacement Map其实与Normal Map和Bump Map也十分类似，后两者都是通过修改物体法线实现逻辑上的改变模型表面；而Displacement Map则是通过修改顶点的位置实现物理上的改变模型的几何形状，因此Displacement Map在提供最真实的效果的同时也会大幅增加渲染性能的开销。

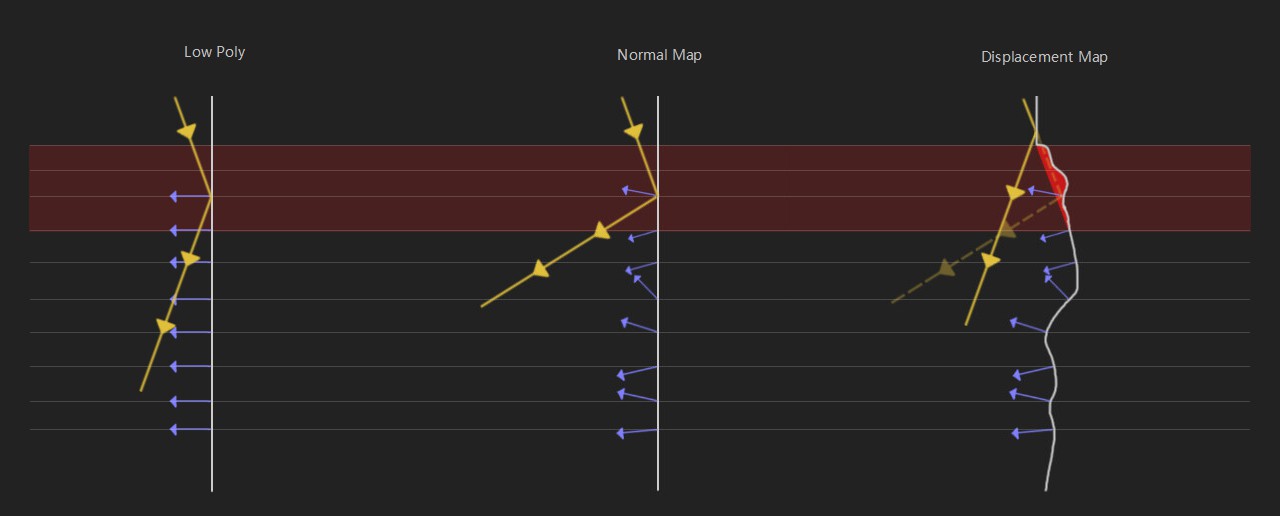
可以通过物体投影的边缘以及自阴影发现这两种贴图的差别：

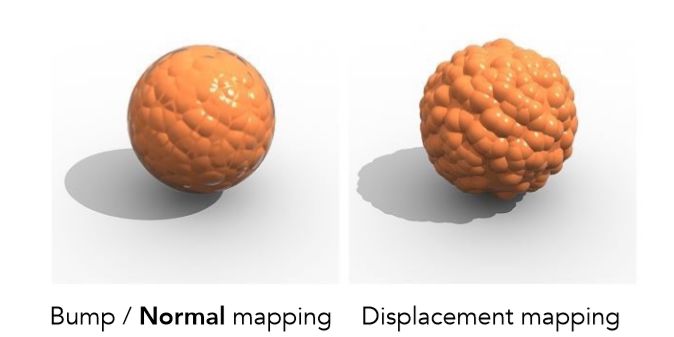
Displacement Map因为是通过改变模型上点的位置实现的，因此又被称为位移贴图。

需要注意的是，Displacement Map要求三角形数量足够多，通常结合曲面细分使用，否则会导致效果不明显。

就实现复杂度/质量与性能开销而言，Dispalcement Map>Normal Map>Bump Map。

 

Vector Displacement Map（矢量置换贴图）

Vector Displacement Map与传统Displacement Map不同的是记录了模型上各点的高度和方向信息，并储存为16/32位浮点颜色信息。

传统的置换贴图使用的是低模的UV坐标，贴图记录了高模和低模之间的差异；而矢量置换贴图在使用类似映射方法的同时，还能在空间中移动顶点。因此也能记录复杂的凹面下（如蘑菇、耳朵等）的顶点信息，将雕刻细节从一个模型转移到另一个模型。

以这个蘑菇为例：传统的置换贴图只能做到改变其高度，但是用矢量置换贴图可以实现更接近原始造型的效果。

 

本文参考自本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记以及Zanple的游戏资源中常见的贴图类型，感谢。

你太习惯这个世界了，
才会对任何事情都不感到惊奇。

《苏菲的世界》
——乔斯坦·贾德