前言

之前有更新过光照模型基础的系列文章，例如光照模型基础之Lambert和光照模型基础之Phong与Blinn-Phong，不过这些文章更注重于在游戏引擎中的实现，因此本文就详细介绍一下Blinn-Phong光照模型的具体原理。

Shading

所谓的Shading，指的是对光栅化后的片元进行着色的过程，简单来说就是计算出每个采样像素点的颜色是什么，首先看下面这张图。

这个茶杯的光照，大体分为三种类型：

1. 第一部分是高光（Specular highlights），最亮的部分，明暗变化相对剧烈；
2. 第二部分是漫反射（Diffuse reflection），明暗变化相对不是那么明显；
3. 第三部分是环境光（Ambient lighting），没有明暗变化，如图光从右侧打过来，按理说左侧应该是黑色的阴影，但是由于光在环境中反射，被反射到了这个杯子的背面而被照亮。

这就是经典的Phong光照模型的构成，需要注意的是这种光照模型只是经验模型，并不是真正物理准确的模型，但是优点是计算快，效果可以接受，因此至今依然广泛的运用在各种游戏之中。

下面会介绍每种光照类型的详细原理，注意以下提到的所有方向向量皆为单位向量。

环境光

首先从最简单的环境光开始，用一个简单的式子就可以表示

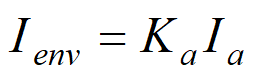
其中Ka代表物体表面对环境光的反射率，Ia代表入射环境光的亮度，Ienv存储结果，即人眼所能看到从物体表面反射的环境光的亮度。效果如下：

环境光是一个纯经验的计算模型，只能看到一个物体的平面形状，没有任何明暗变化和细节，只是用来模拟间接光照，避免阴影处死黑一片。

其中反射率和光的亮度都是一个3维的RGB向量，一个物体能够有颜色，其实就是因为它吸收了一定颜色的光，将剩下的光反射到人眼，从而就有了颜色。

漫反射

漫反射便是光从一定角度入射之后从入射点向四面八方反射，且每个不同方向反射的光的强度相等，而产生漫反射的原因是物体表面的粗糙，导致了这种物理现象的发生。

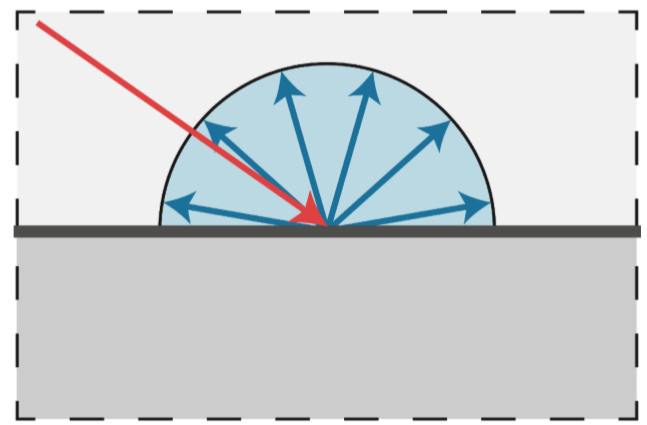
要模拟这种漫反射，首先应该考虑入射的角度所造成的接收到光强的损失，如下图所示：

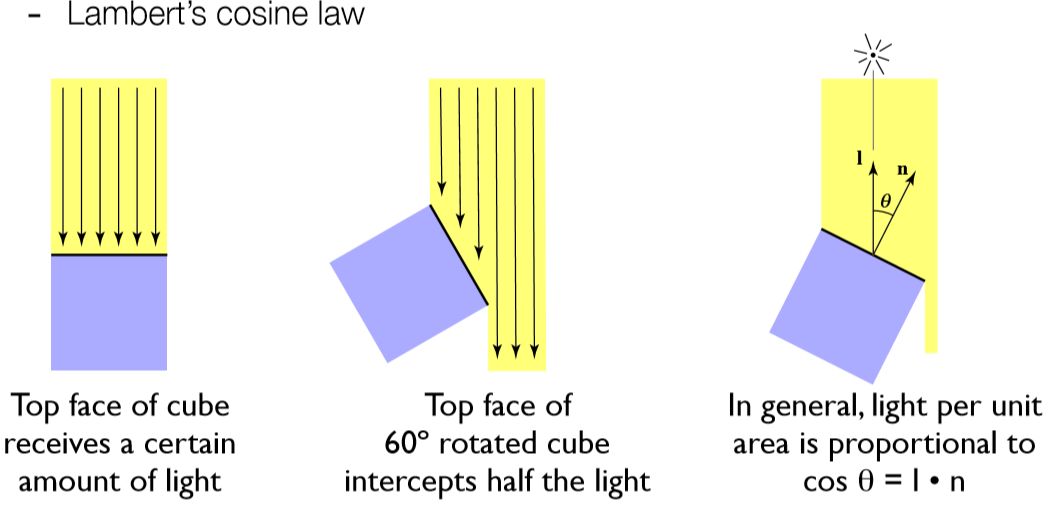
只有当入射光线与平面垂直的时候才能完整的接受所有光的能量，而入射角度越倾斜损失的能量越大，具体来说，我们应该将光强乘上一个cosθ=l · n，其中l为入射光方向，n为平面法线方向。

除了入射角度之外，光源与照射点的距离也应该考虑，直观来说，离得越远当然强度也就越弱！具体来说如图所示：

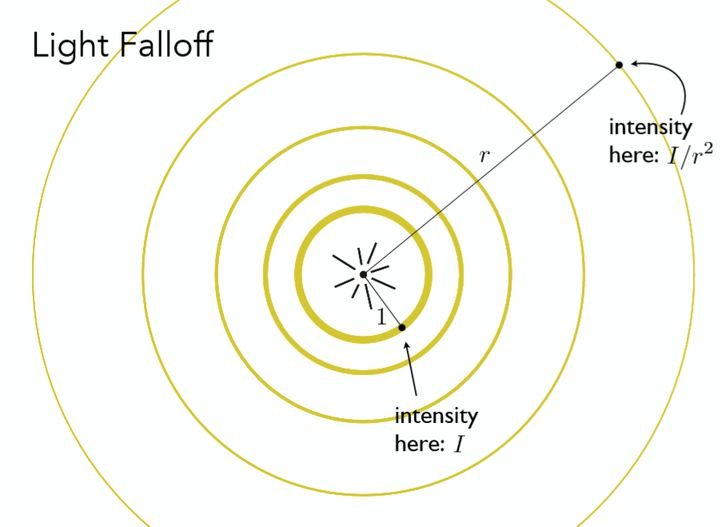
图中中心为一个点光源，光线均匀的向周围发射，可以想象光源发射出来的能量其实是一定的，那么在任意两个球面上接受到的能量之和一定相等。而离圆心越远，球面的面积越大，单位面积所接受能量也就越弱。

由于球面面积公式为4πr²，距离为1时，球壳上某点的光的强度为I；距离为r时，球壳上某点的光照强度：4πI=4πr²×I’ 解得I’=I/r²，因此光强I应该除以半径的平方。

这样就可以较为正确的去模拟漫反射了！如下式：

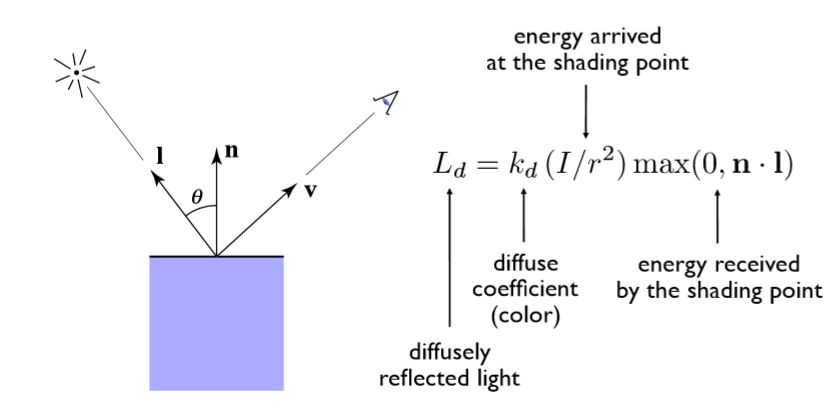
其中Kd为漫反射系数，I为入射光强，n和l分别如图中所示为法线向量和入射方向，max函数是为了剔除平面背面照射过来的光，避免得到负数亮度。

同样漫反射系数和入射光也是三维的RGB色彩向量，决定了最后的漫反射颜色。

另外从公式中可以看出漫反射光线强度是与反射方向无关的，因此无论人眼在哪观察接收到的强度都是一样的！

而将上面的环境光和漫反射叠加起来，得到的就是经典的Lambert光照模型了。

高光

对于高光反射来说，除了考虑漫反射中提到的光源到反射点的距离r之外，需要注意的是，观察方向在镜面反射时是很重要的，具体来说，只有当观察方向集中在反射方向周围很近的时候才能看见反射光，因此在镜面反射中会考虑R与v的夹角α。如下式：

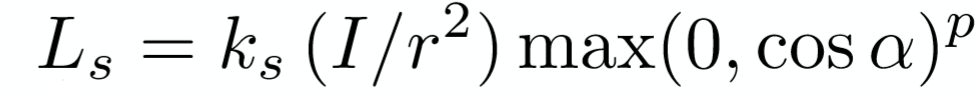
其中Ks为镜面反射系数，I为入射光强，r为光源到入射点距离，注意这里在max剔除背面的光之后，还乘了一个指数p，添加该项的原因很直接，因为高光的范围应该是很小的，需要一个指数p加速衰减。

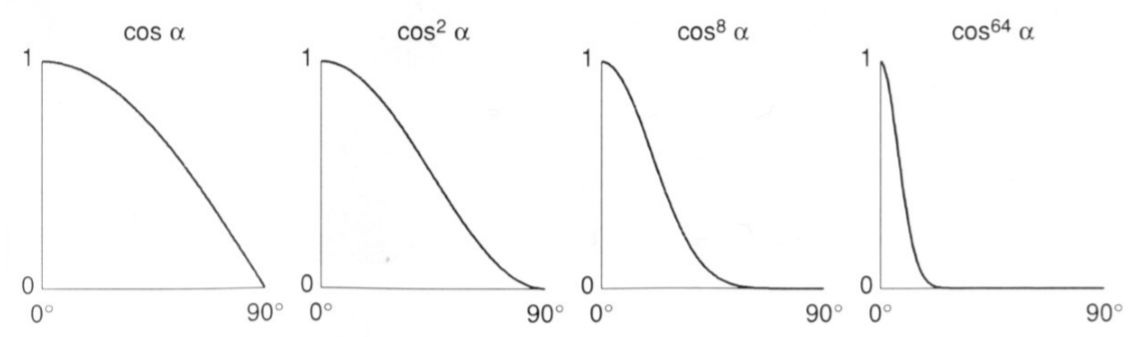
将环境光、漫反射、高光叠加到一起，就可以得到Phong光照模型的效果了。

Blinn-Phong

Blinn-Phong反射模型只是对phong模型高光部分计算方法的一个优化。

具体来说就是因为反射向量不好计算，所以将反射方向与人眼观察方向夹角简化成如下图所示的一个半程向量和法线向量的夹角。

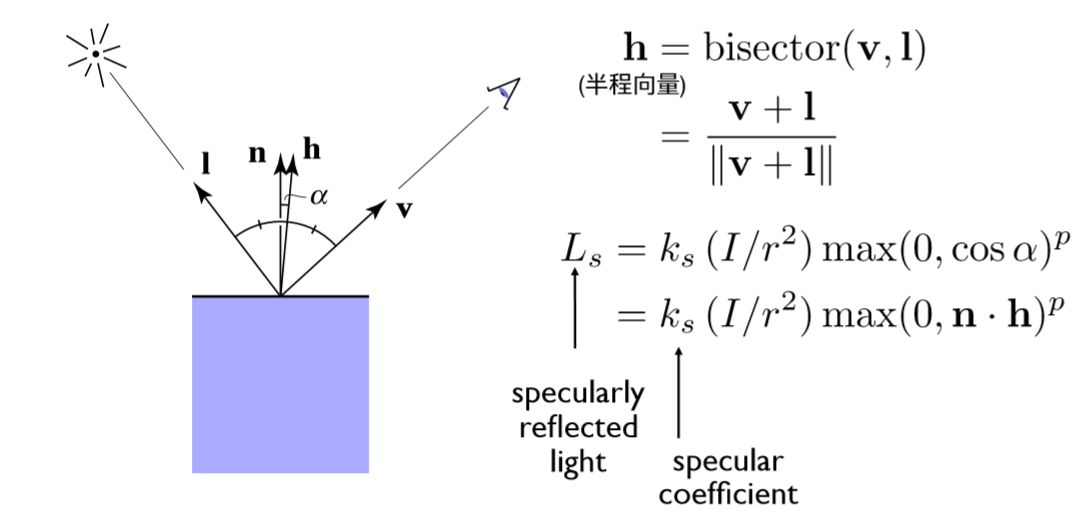
半程向量（h）：入射方向l和出射方向v的角平分线 （h的方向很好算，由于l和v都是单位向量，根据平行四边形法则，h=l+v，再将h归一化将长度变成1即可）。

这样的得到的结果其实是与真实计算反射与人眼观察夹角的结果是非常近似的(具体来说该角度是正确角度的一半)，但好处在于大大加速了计算的速度，提升了效率！

本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》以及孙小磊的计算机图形学系列笔记，感谢。

我一边踉跄前行，
一边重整旗鼓。

——太宰治