前言

贝塞尔曲线(Bézier Curves)，从名字就可以看出不是英文名词，是一个法国工程师皮埃尔·贝济埃（Pierre Bézier）广泛发表，用于设计汽车车身曲面的算法。

贝塞尔曲线有着很多特殊的性质，在图形设计和路径规划中应用都非常广泛，贝塞尔曲线完全由其控制点决定其形状,　ｎ个控制点对应着ｎ－１阶的贝塞尔曲线，并且可以通过递归的方式来绘制（划重点啊，递归）。

 

贝塞尔曲线(Bézier Curves)

首先看一下贝塞尔曲线是如何绘制的

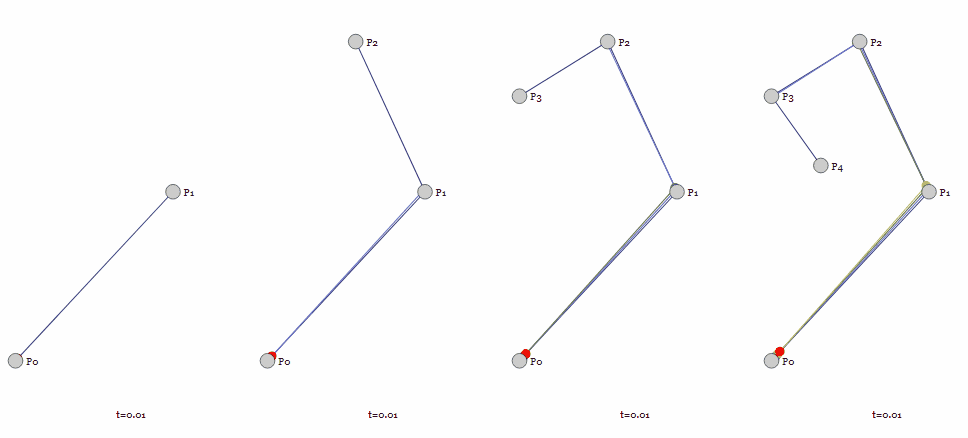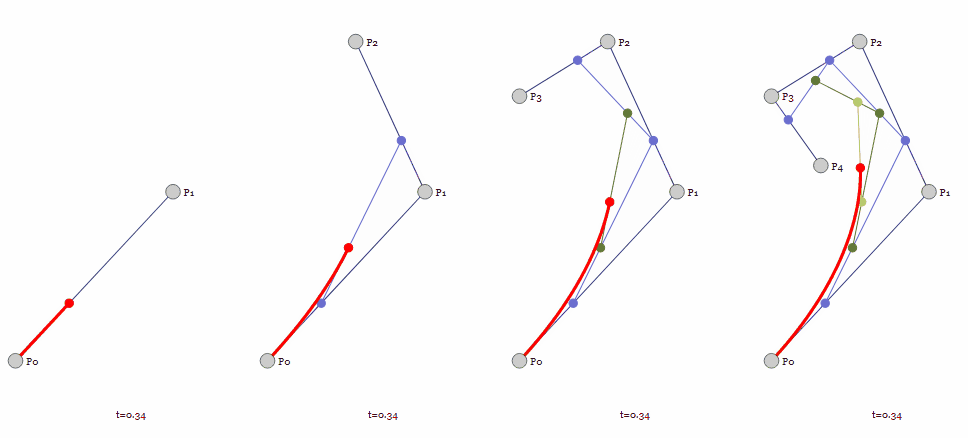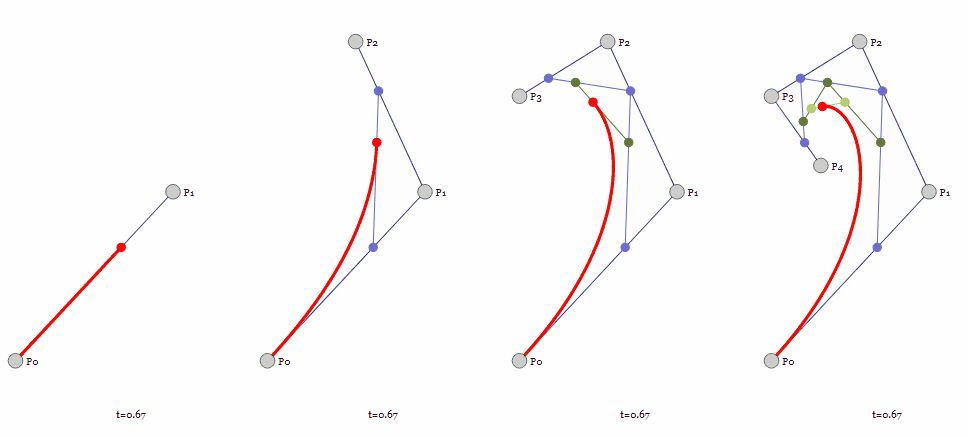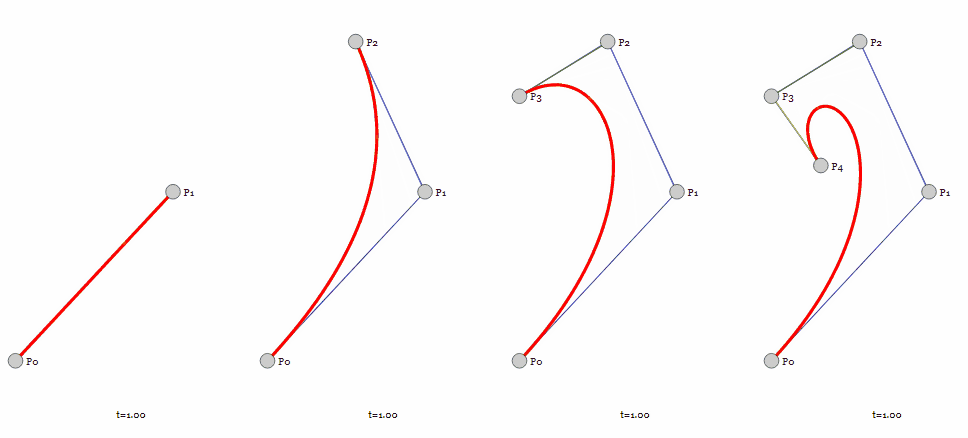
上图来自Jason Davies，该页面的控制点是可以自由移动的，可以去玩一下感受控制点位置对于曲线形状的影响。

贝塞尔曲线的定义很像参数方程，给定一个参数t取值范围为[0, 1]，给定t一个值就能确定贝塞尔曲线上的一点，将所有得到的点连续起来，就能得到完整的贝塞尔曲线。

 

一阶贝塞尔曲线

首先从两个控制点构成的一阶贝塞尔曲线开始。

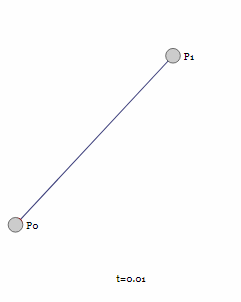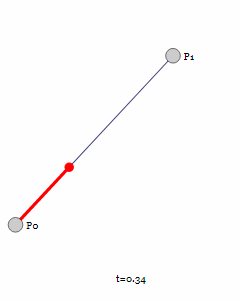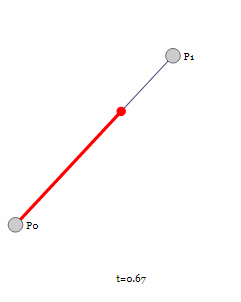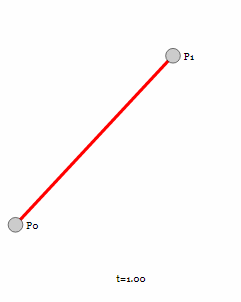
对于一阶贝塞尔曲线为我们可以看到是一条直线，通过几何知识，很容易根据t的值得出线段上那个点的坐标：

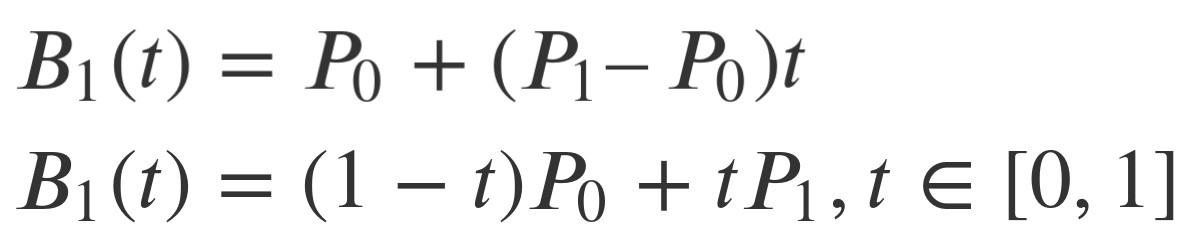
一阶贝塞尔曲线很好理解，就是根据t进行的线性插值。

 

二阶贝塞尔曲线

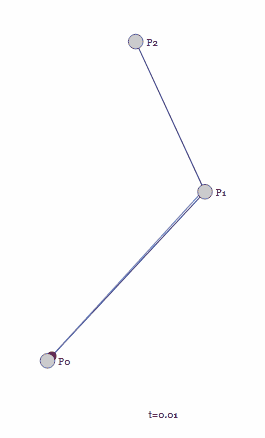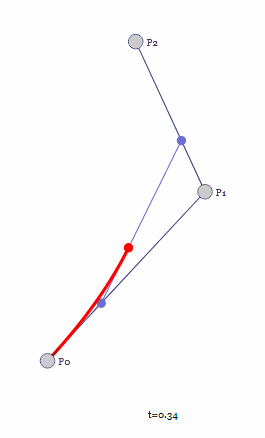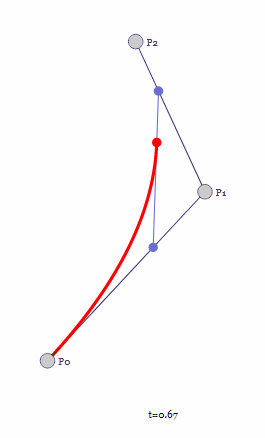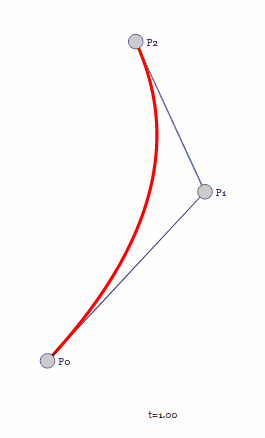
接下来是三个控制点构成的二阶贝塞尔曲线，文章开头说过贝塞尔曲线的重点是递归，因此二阶贝塞尔曲线必然和一阶贝塞尔曲线有关系。

对于取值范围为[0, 1]的参数t，先通过线性插值得到线段P0P1上面的点t0，再通过线性插值得到线段P1P2上面的点t1，t0t1构成的线段进行线性插值得到最终的贝塞尔曲线上当前t值下点的位置。

显然随着t的取值变化，t0t1构成的直线也是在不断变化的，最终得到的就是一条平滑的曲线。

 

 

三阶及更高阶贝塞尔曲线

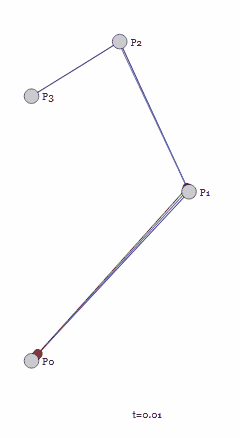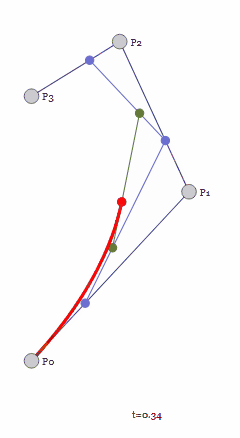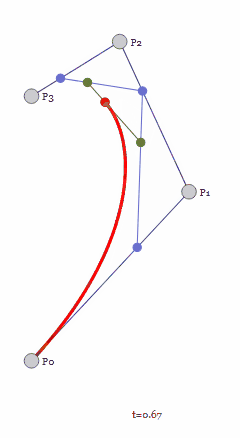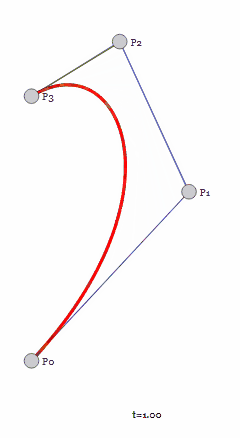
四个控制点构成的三阶贝塞尔曲线也类似，先求出不断变化的二阶控制点，再得到不断变化的一阶直线，最后进行线性插值即可。

再将该方法扩展到更高阶也同理，都是对于任意取值的t（取值范围[0, 1]），通过多次线性插值递归地降阶，求低阶控制点位置，最后得到一阶的直线做线性插值，整个过程类似于对复杂函数不断求导，直到得到确定的值。

另外还可以观察到曲线会和初始控制点与终止控制点相切，出现在当t值取0或1这样的极限值时。

 

贝塞尔曲线方程及性质

以3个控制点为例，将贝塞尔曲线方程完全展开看看

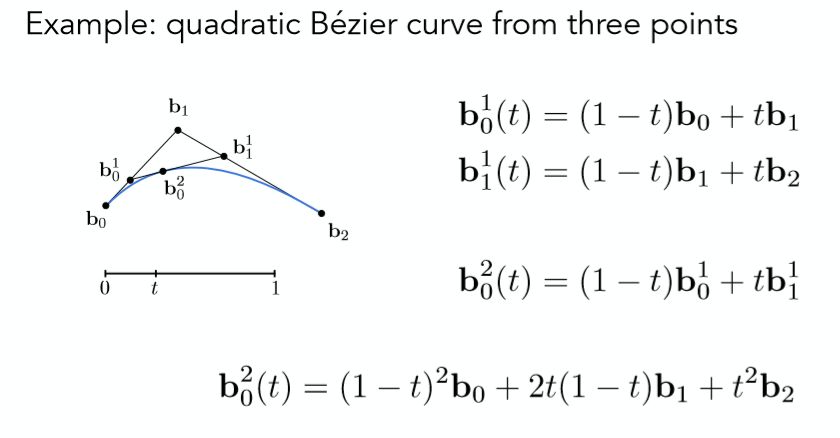
其实看到这就已经非常清楚了，最终得到的贝塞尔曲线方程恰好就是一个关于参数 t 的二次方程，如果细心观察的话，其实可以发现每个控制点对应的系数是非常有规律的，系数是二项数的展开，因此可以总结规律得到一个任意控制点组成的贝塞尔曲线的方程如下:

对于这样一个特殊系数其实也有一个多项式与之对应，正是伯恩斯坦多项式，其定义如下图所示。

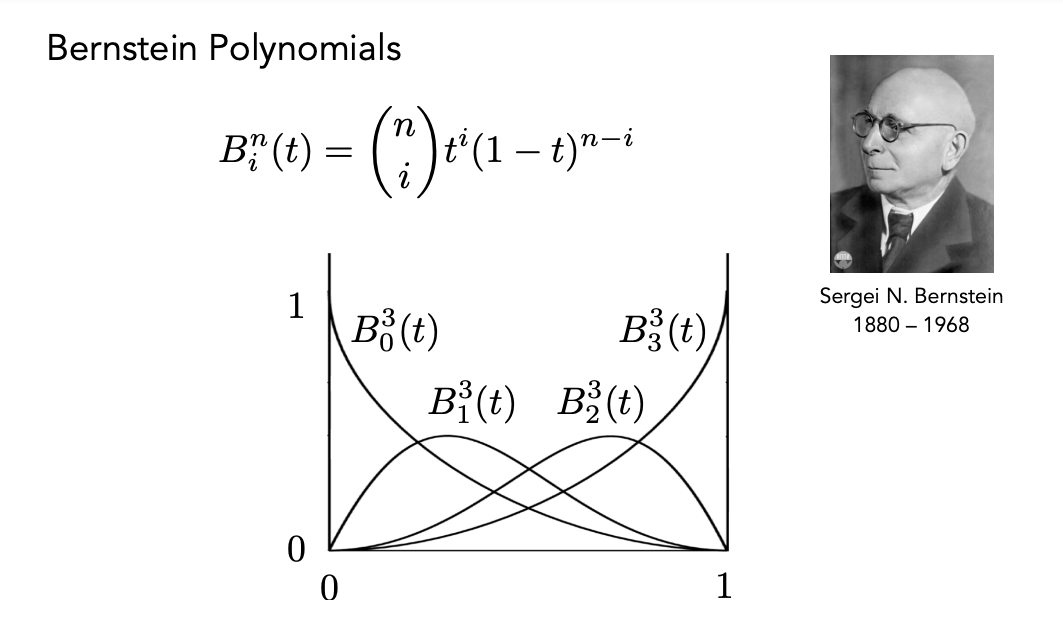
因此贝赛尔曲线的每个控制点对应多项式的一项，并且所有项的系数相加等于1，这也说明了为什么当t值取0或1这样的极限值时曲线会经过起始控制点与终止控制点。

最后对贝塞尔曲线的几点性质做一个概括:

1 必定经过起始控制点和终止控制点并与起始控制点和终止控制点相切。

2 具有仿射变换性质，可以通过变换所有控制点位置实现整条曲线的变换（不能用于投影变换）。

3 凸包性质（Convex Hull），曲线一定不会超出所有控制点构成的凸多边形范围，可以理解为用橡皮筋围住木板上的多个钉子。

 

分段贝塞尔曲线（Piecewice Bézier Curves）

对于高阶贝塞尔曲线它有一个严重的缺陷:

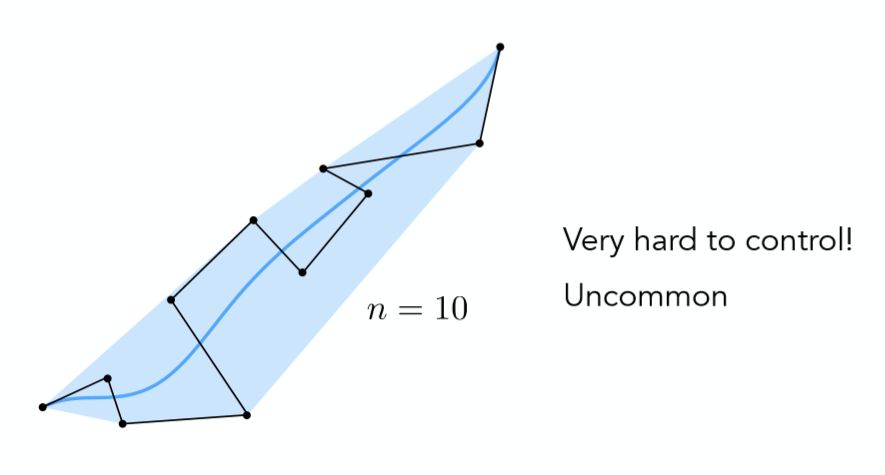
对于上图所示的由11个控制点所得到的10阶贝塞尔曲线，由于控制点众多，很难控制局部的贝塞尔曲线形状，因此为了解决该问题，有人提出了分段贝塞尔曲线，即将一条高阶曲线分成多条低阶曲线的拼接。

其中用的最多的就是3次贝塞尔曲线（Piecewice Cubic Bézier Curves），每4个控制点定义一条曲线，首尾的两个控制点定义曲线的两端位置，中间的两个控制点定义曲线的弯曲度，最后将多段曲线拼接，如下图:

从代数意义上，两段曲线连续，就是两段曲线在连接处相等，连接处可能是尖锐的角，一般称为C0连续或者位置连续。

如果想要使得拼接的点看起来较为平滑的话，还要满足C1连续，即连接点的切线相同，两段曲线的一阶导数在连接处相等，可以简单理解为曲线连接点和两旁的控制点三点共线且等距，C1连续也被称为斜率连续。（与C1连续类似的是G1连续，要求切线方向一致即可，大小不必相等，即曲线连接点和两旁的控制点三点共线。）

在C1连续的基础上还有C2连续，即两段曲线的二阶导数在连接处相等，能够更加平滑，C2连续也被称为曲率连续。

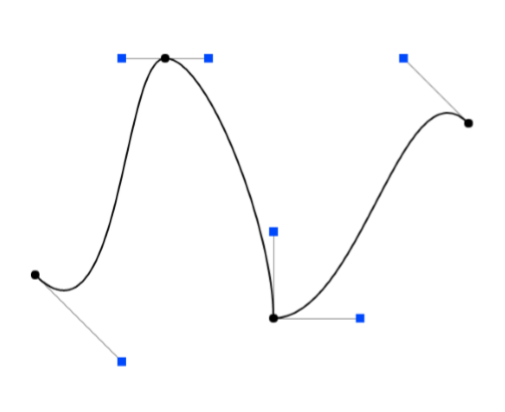
上图来自一个贝塞尔曲线的网页demo，也可以去玩玩。

PS等具有画图功能的软件中的钢笔工具所运用的便是这种3次分段贝塞尔曲线，还在许多字体或是矢量图的设计中广泛使用。

 

贝塞尔曲面(Bézier Surfaces)

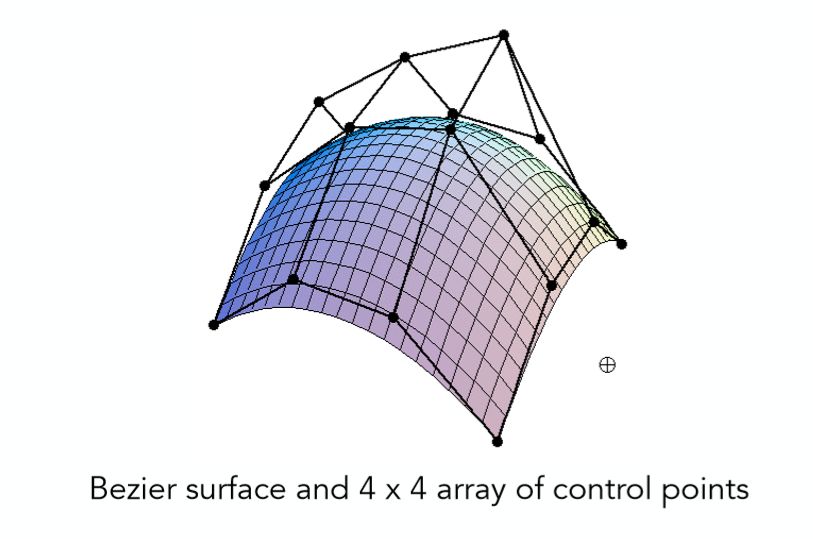
其实在理解了贝塞尔曲线之后，贝塞尔曲面的原理也是十分容易理解的了，无非是一个从2维到3维的过渡。

如果说对于曲线来说只有一个参数 t ，那么对于一个面来说，就应该有两个参数，分别设 u，v，取值范围为[0, 1]，具体过程如下图所示:

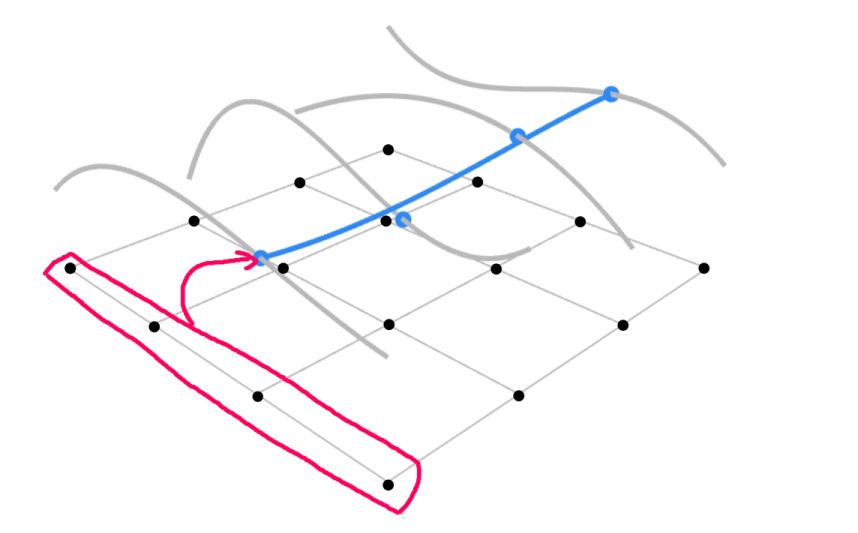
首先规定一共4×4 = 16个控制点，其水平面位置如图中16个黑点所示(并未表示出高度，防止图形太乱)，将这16个点分成4列，图中红色圈中的为一列的具体例子。

第1步 在这4个控制点之下利用第一个参数 u 运用第一章的计算贝塞尔曲线的方法得到蓝色点，因为有4列，所以一共可以得到如图所示的4个蓝色点。(灰色曲线分别为每列4个点所对应的贝塞尔曲线)

第2步 在得到4个蓝色顶点之后，在这四个蓝色顶点的基础之下利用第二个参数 v 便可以成功得出贝塞尔曲面上的正确一点

第3步 遍历所有的 u，v值就可以成功得到一个贝塞尔曲面。

 

本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记，感谢。

凡有的，还要加给他，叫他有余；
凡没有的，连他所有的也要夺去。

——《圣经·马太福音》