前言

曲面细分是指将一个模型的面合理的分成更多小的面并相应调整位置，从而得到更加平滑的模型，通过更高的模型精度提升渲染效果。

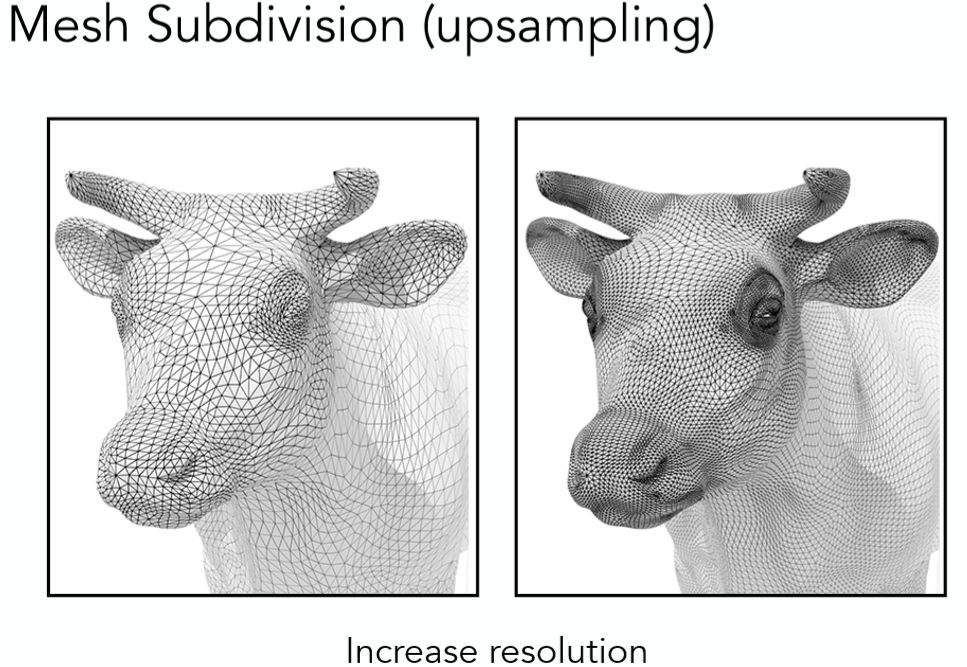
曲面简化是指将一个模型的面合理的合并成更少的面，从而在保证模型整体结构的同时降低模型精度，在特定情形下加快渲染速度使用(如通过LOD技术减少远处的复杂模型参与渲染计算的面数)。

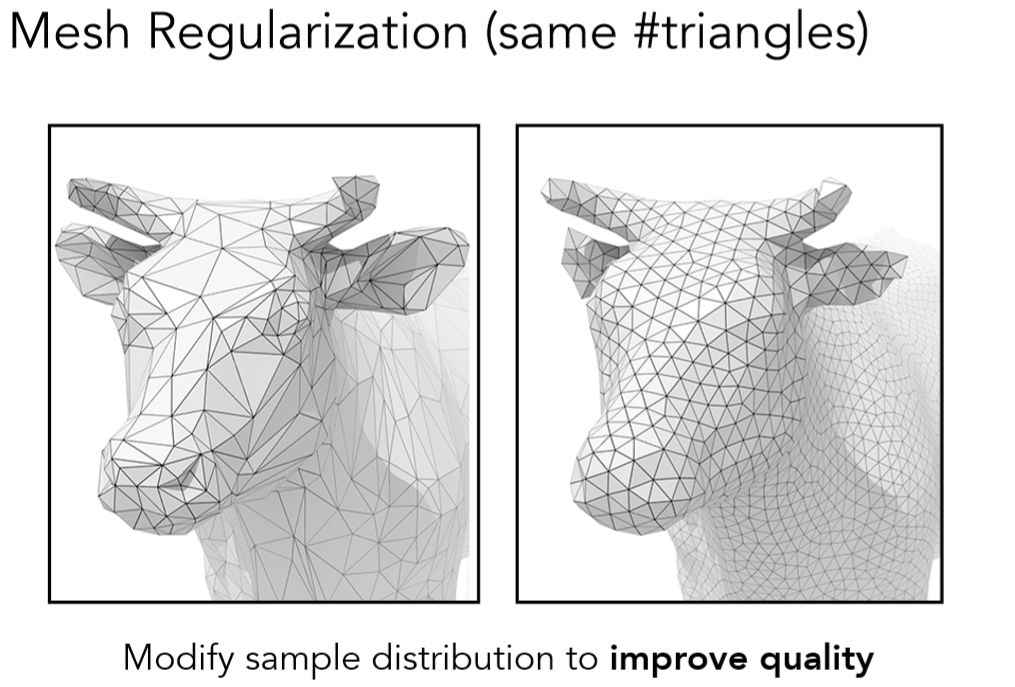
除了细分与简化之外，还有另外一种同属一类的操作叫做曲面规则化（Mesh Regularization），其所作的便是在尽量少丢失细节下将三角面都变成大小相近的正三角形，从而优化渲染效果的目的，对于该类技术本文不做详解。

 

曲面细分(subdivision)

Loop细分(Loop Subdivision)

Loop细分是一种专门针对三角形面的细分方法，其核心步骤也十分容易理解。注意Loop是发明这种算法的人的姓氏，不是循环的意思。

1 生成更多顶点和三角形

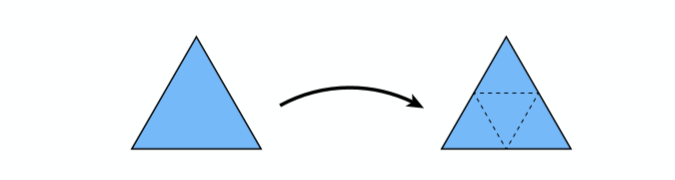
如图所示，在每条边的中点处生成新的顶点，并连接每条边的中点生成一个新的三角形，原来的三角形就会被分割成4个三角形。

2 调整顶点的位置

将所有的顶点分为两类，一类是新生成的顶点，一类是原来就有的旧顶点，对于新生成的顶点做如下处理：

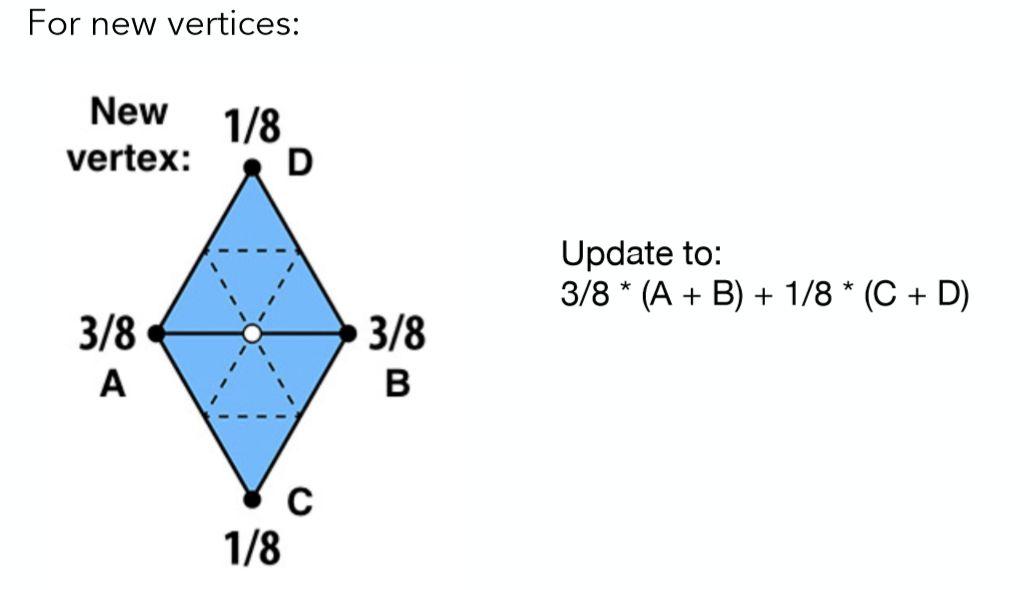
这里新的顶点就是白色的那个顶点，会被两个原来的三角形所共享，将共享顶点所在的这条边两端的两个旧的顶点分别定义为A、B，这两个三角形不共边的两个顶点分别定义为C、D，然后将共享顶点（上图白色点）的位置调整为3/8 * (A + B) + 1/8 * (C + D)即可（这个公式其实就是一个简单的加权平均，A和B离共享顶点近一些，所以占的比例相对较大，而C和D离共享顶点远一些，所以占的比例相对较小）。

对于旧的顶点，做如下处理：

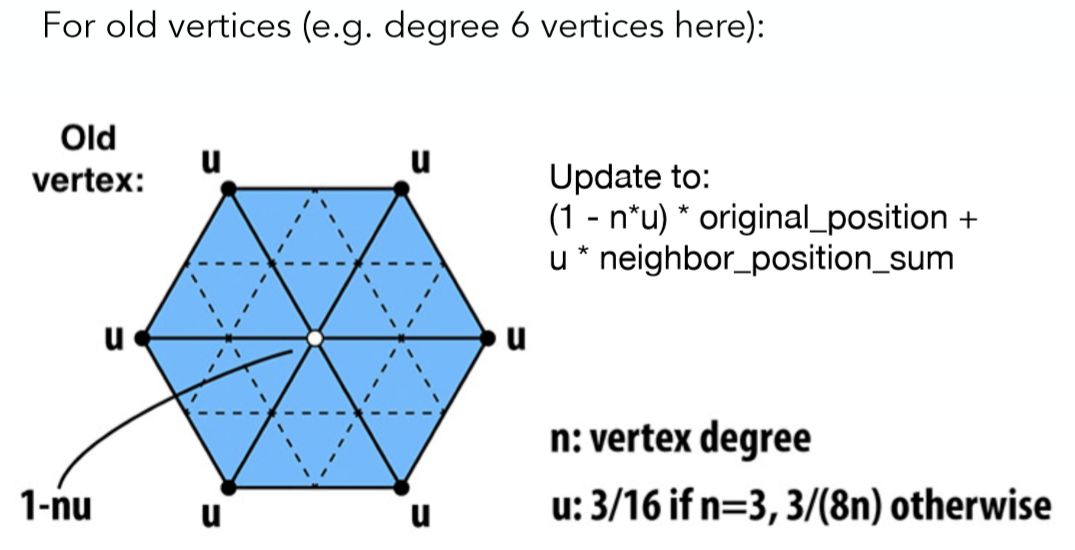
对于旧的顶点（如上图白色点），周围的旧顶点会对这个顶点有一定的影响。Loop细分规定这个要计算的旧顶点（上图白色点）一部分受周围旧顶点的影响，一部分保持自己的位置属性。

在这里我们定义一个n，为顶点的度（这个顶点连接的边的数量），再定义一个u，这个u仅仅是一个与顶点的度有关的数。最终的计算公式如下：

(1 – n*u) * original_position + u * neighbor_position_sum

从这个公式可以看到，当顶点的度很大（连接了很多三角形），那么这个顶点基本就可以由周围的旧顶点决定位置，当顶点的度很小（连接的三角形很少），那么这个顶点原来位置的权重就会很大。

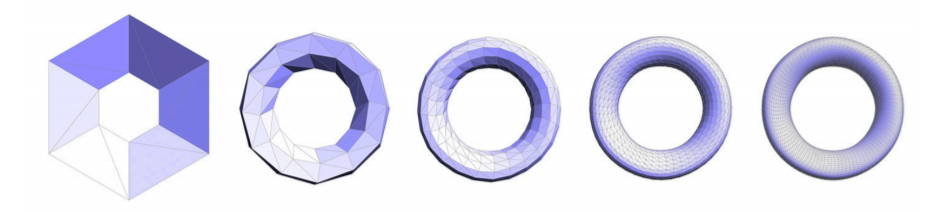
以上就是Loop细分的全过程了，最后看看效果： (这是一个不断进行Loop细分的例子)

 

Catmull-Clark细分(Catmull-Clark Subdivision)

正如上文所说Loop细分针对是所有三角形面，那么对于不仅仅只有三角形面该怎么办呢？这也就有了Catmull-Clark细分，这里以四边形面和三角面的混合为例： 首先做一些定义：

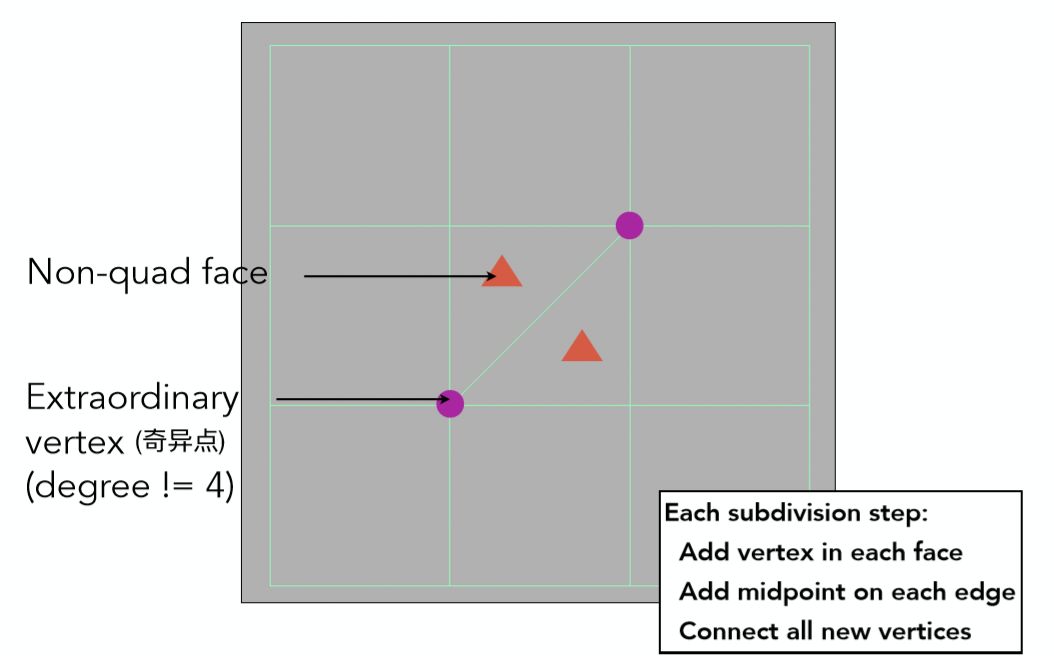
1 对于所有不是四边形的面，称之为Non-quad face

2 所有度不为4的顶点称之为奇异点

3 每次细分步骤如下图所示，在每个面中心都添加一个顶点，在每条边的中点也都添加一个点，面中心的新顶点连接所有边上的新顶点，结果如下图所示：

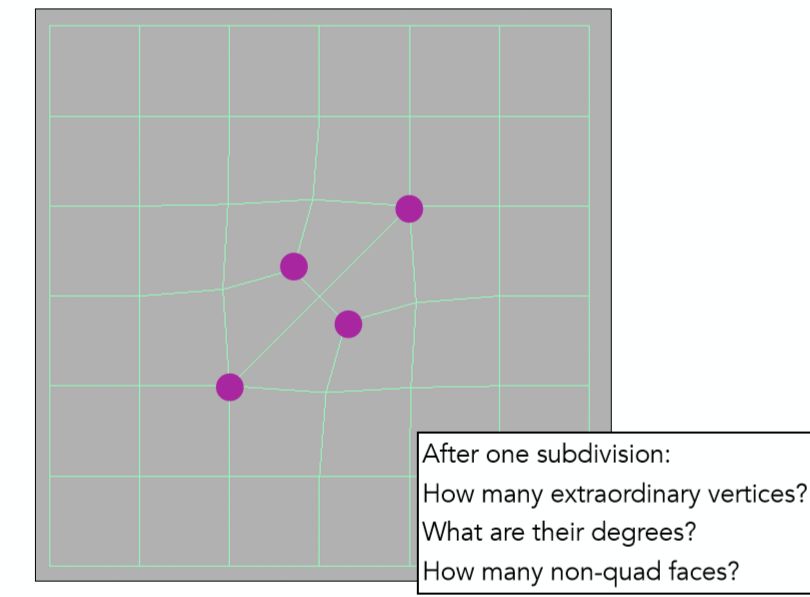
考虑右下角几个问题，其实也是一些Catmull-Clark细分的特点

1 有几个非四边形面，就会多出几个奇异点，所以现在一共有2+2 = 4个

2 新多出来的奇异点的度数与原来所在面的边数相等，如这里就是3度

3 第一次细分之后所有面都会变成四边形，且往后奇异点数目不再增加

这里给出一个再一次细分的结果：

可以看到奇异点依然是4个，不再改变。

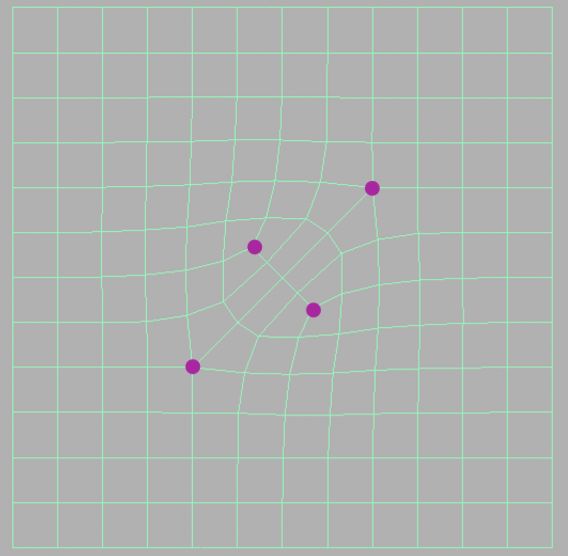
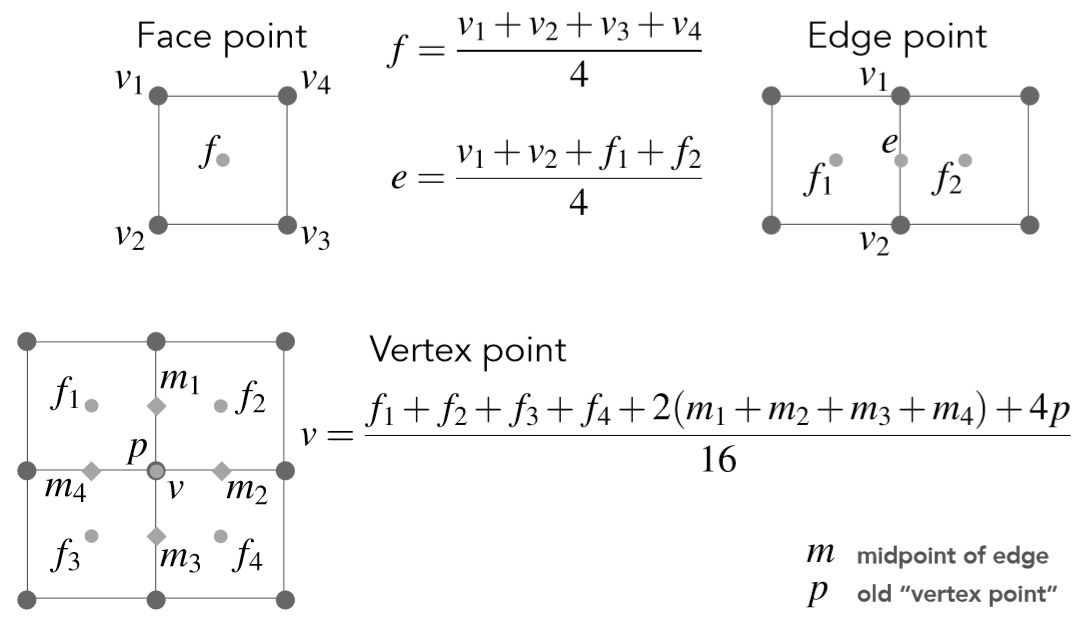
以上我们明白了如何增加新顶点，与Loop细分类似，同样需要去调整各类顶点的位置，这里将所有顶点的更新分为三种，第一种是对于面的中心点f的更新，第二种是对于边的中心点e的更新，第三种是对于老的顶点v的更新。

对于各类顶点位置调整如下图所示：

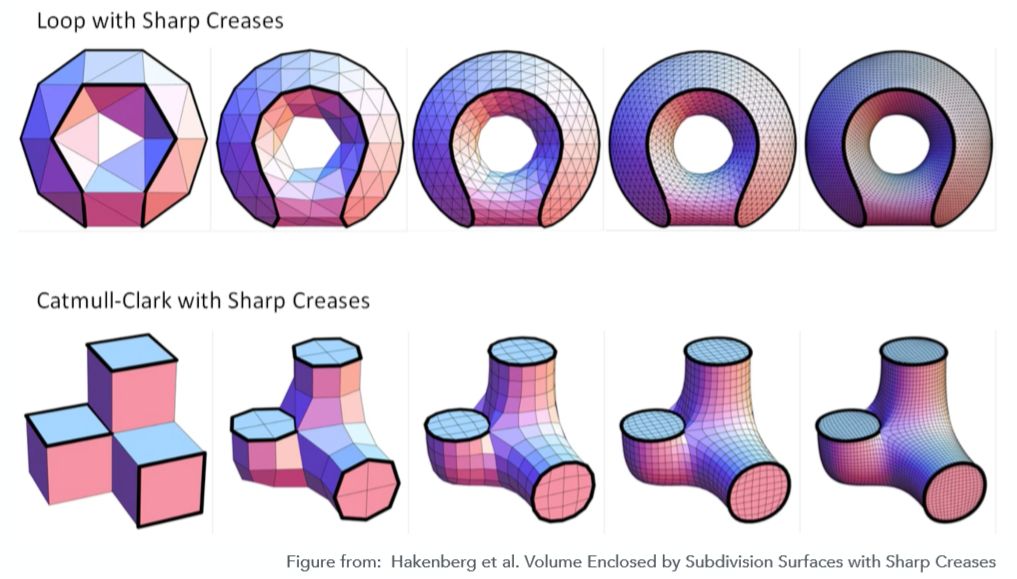
Loop细分 V.S Catmull-Clark细分：

 

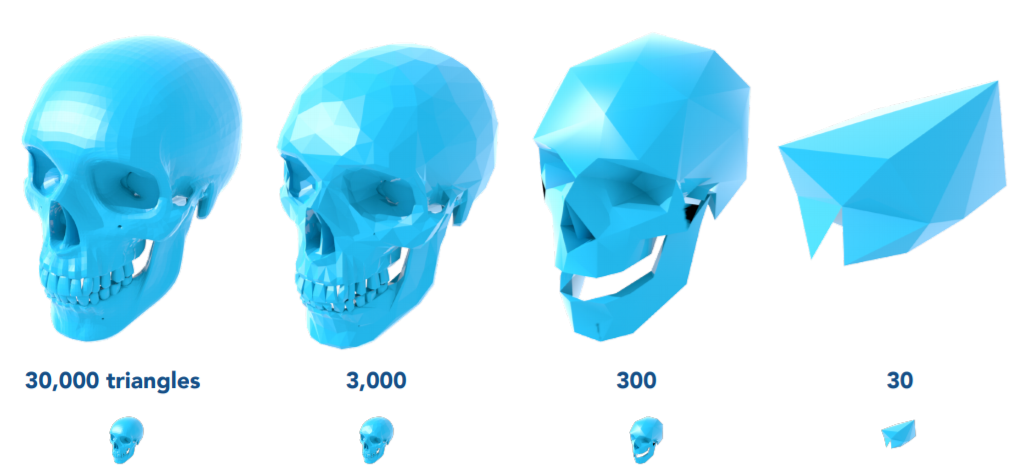
曲面简化(Smplication)

曲面简化所利用的一个方法叫做边坍缩，如下图所示就是将一条边的两个顶点合成为一个顶点。

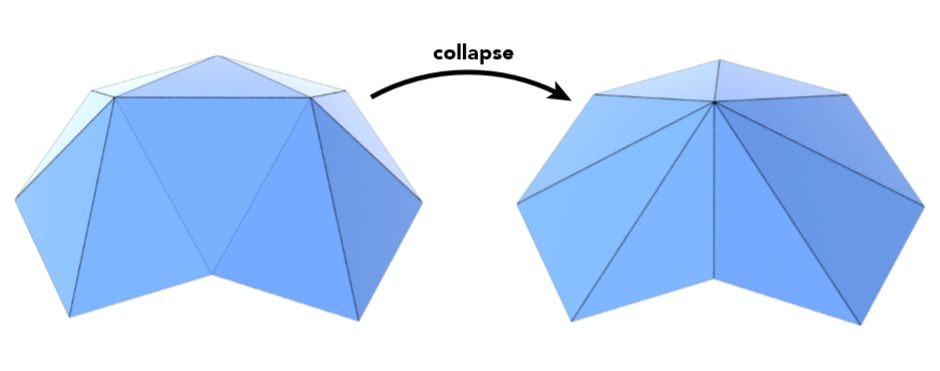
但随之而来的问题就是，曲面简化需要尽量保持原本模型的基本轮廓，如何坍缩一条边，或者说坍缩哪一条边能够使得原模型样貌被改变的程度最小，这就是曲面简化的关键所在。

为此引入一个度量，即二次误差度量(Quadric Error Metrics)。

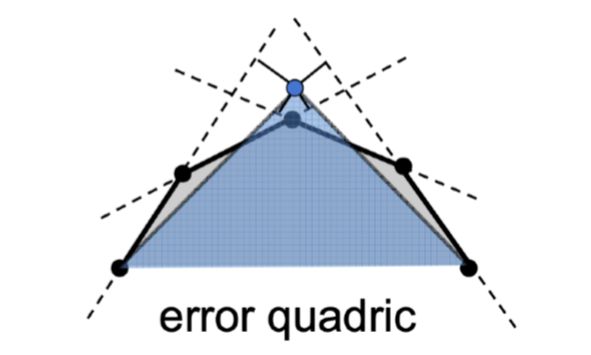
把这个新生成的顶点放置在某个位置上，使得这个顶点到原来相关联的各个面的距离的平方和达到最小（上图中的边代表三角面）。如果能够使得这个误差最小那么对整个模型样貌修改一定程度上也会较小。

对于整个模型有很多条边，假设如果坍缩一条边，并且算出把这个坍缩后的点放在最佳的位置上会得到一个多大的二次度量误差。对于整个模型而言，每次肯定都是要坍缩二次度量误差最小的边。

那么其实到这整个曲面简化的算法流程已经比较清晰了。

1 为模型每条边赋值，其值为坍缩这条边之后，代替两个老顶点的新顶点所能得到的最小二次误差度量。

2 选取权值最小的边做坍缩，新顶点位置为原来计算得出使得二次误差最小的位置。

3 坍缩完之后，与之相连其他的边的位置会改动，更新这些边的权值。

4 重复上述步骤，直到到达终止条件

但是问题是，如果坍缩了一条边，会有一些临近边的位置要跟着这条坍缩的边变化，那么这些边的二次度量误差就会随之发生变化。

因此这里要通过一种数据结构，既可以每次取到二次度量误差的最小值的边，又可以动态地以最小的代价去更新其他的受影响的元素。那么这里要使用的数据结构就是堆（优先队列）。

这其实是一个标准的贪心算法，可能到不了全局最优解，但事实证明最终的结果依然相当不错。

 

本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记，感谢。

一个人直到自己为什么而活，
就可以忍受任何一种生活。

——尼采