前言

想要得到一个漂亮准确的场景渲染效果，不只需要物理正确的全局照明算法，也要了解现实中各种物体的表面外观和在图形学中的模拟方式，而物体的外观就是物体材质的外在表现，因此本文就介绍一下现实中存在的各种类型的材质以及内在的原理。

 

材质==BRDF

思考一下，在计算机图形学中，材质是什么？

材质就是光线在物体表面的反射方式，而无论什么材质，必定满足物理正确的渲染方程，那么渲染方程中和光的反射有关的是哪个呢？

只有BRDF一项和光的反射方式有关，因此材质其实就是BRDF。

 

漫反射材质（Diffuse / Lambertian Material）

漫反射材质是比较常见的一种材质，往往出现在粗糙的表面，例如木材等。

对于漫反射材质，任何方向的入射光线照射到表面时，都会向半球方向均匀反射。

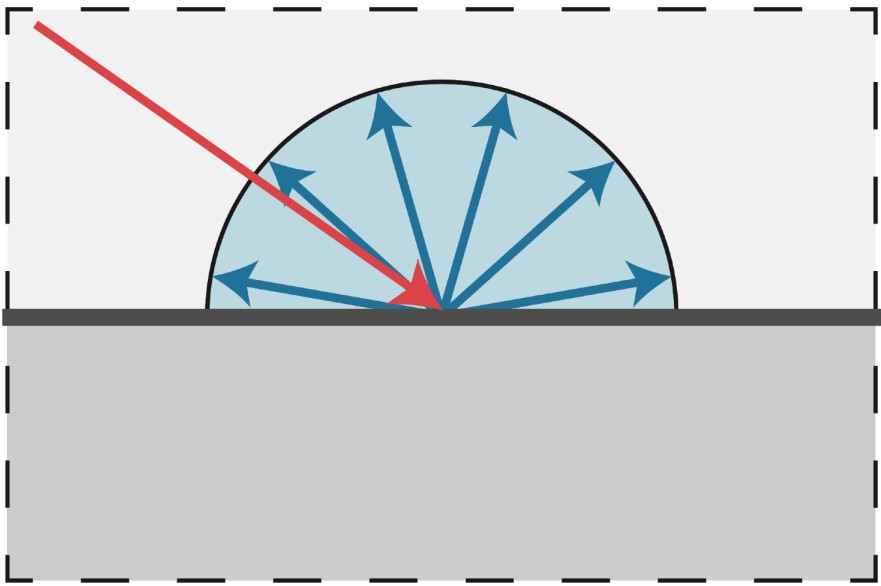
假设该物体是白色的，不发光也不吸收光，且入射的光都是大小相同且方向均匀的，那么根据能量守恒，所有反射出去的光线的能量（Irradiance）等于所有入射光线能量（Irradiance），并且反射的光也是大小相同且方向均匀的。

那么就可以把这个渲染方程写出来。

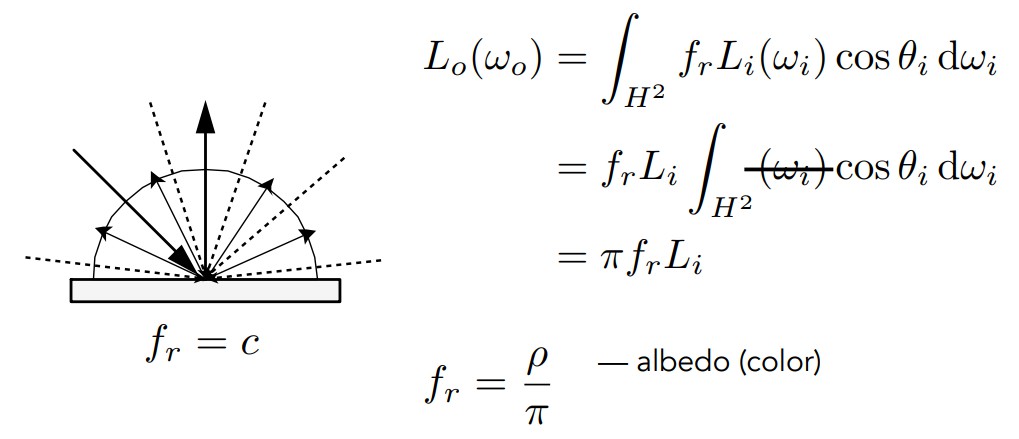
这里入射的Radiance是常数，BRDF（Diffuse）也是常数，这两项就可以拿出去，整个式子就变成了对半球上一个cosθ的积分，积分出来是π。

那么整个式子就变成了 L_o=πf_rL_i ，又因为入射的Radiance等于出射的Radiance，所以 L_i=L_o 。

因此 f_r=1/π。

这时候就是完全不吸收能量的BRDF，这里定义一个反射率albedo（ρ）的概念，这个值可以是一个一维标量，也可以是RGB等三维标量，让反射率albedo在0到1之间，这样就可以引入不同颜色的BRDF，BRDF的值就是albedo / π，取值范围是[0, 1/π]。

 

镜面反射材质（Ideal reflective material）

有完美反射的镜面反射材质，在现实中不多见，例如镜子等。

对于镜面反射材质，入射光线照射到表面后，会沿反射方向反射，入射光线与面法线的夹角等于反射光线与面法线的夹角。

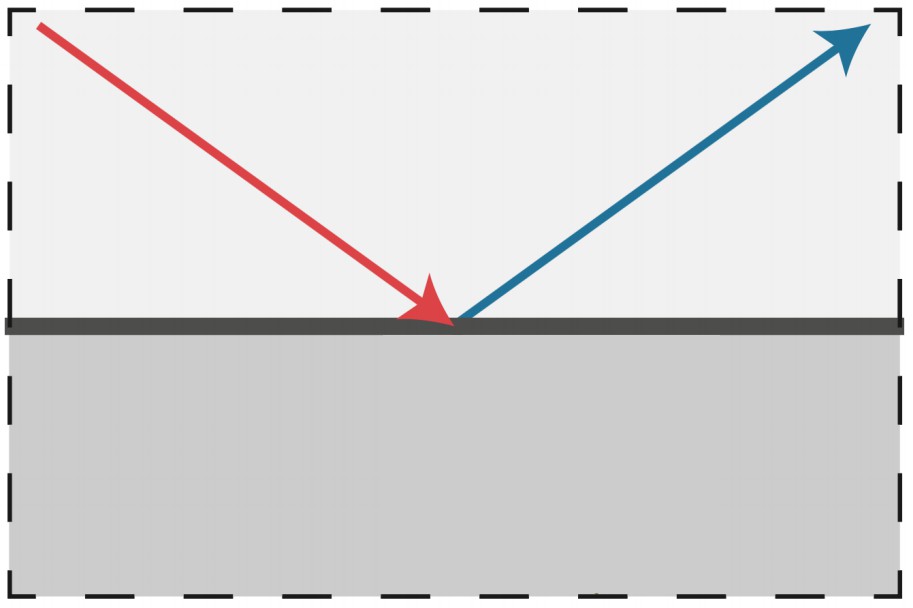
反射方向计算相对容易，如下图所示，已知 入射光ω_i、入射角θ_i、法线方向n，求反射光ω_o。

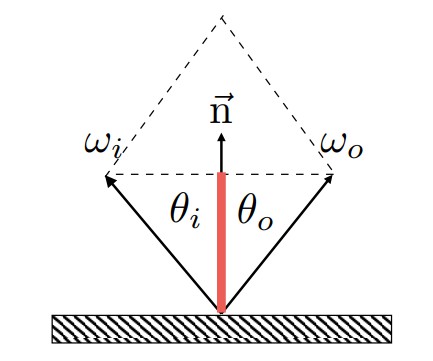
根据向量的平行四边形法则，入射光ω_i加反射光ω_o的结果为入射光在法线方向的投影的2倍，因此可得

 

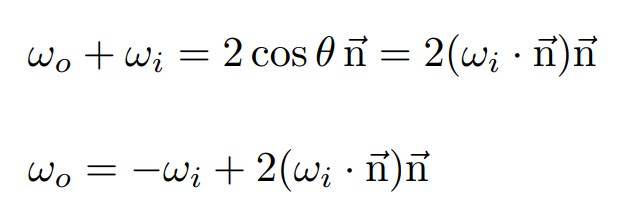
光泽反射材质（Glossy material ）

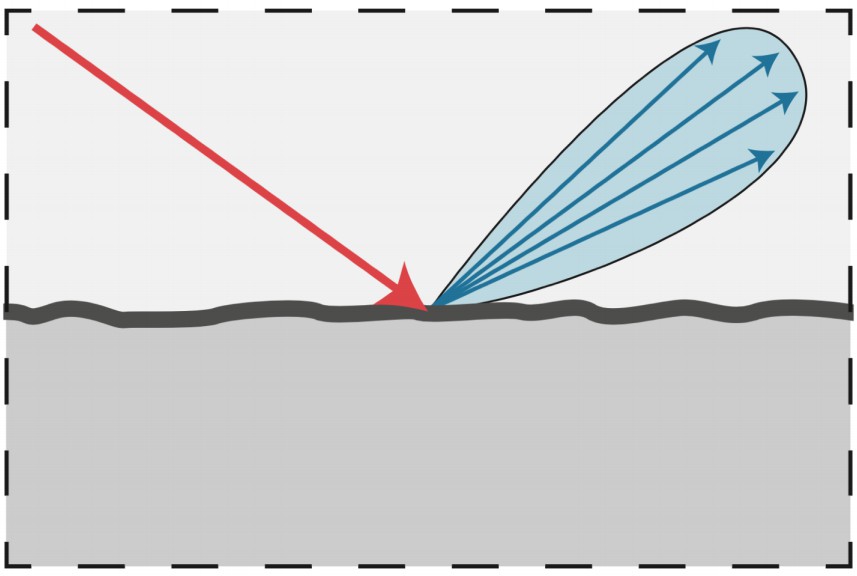
光泽反射材质也比较常见，介于漫反射与镜面反射之间，例如抛光金属等。

对于光泽反射材质，入射光线照射到表面时，会沿反射方向的一定范围内反射。

 

折射材质（refractive material）

折射材质也比较多见，例如水、玻璃等。

折射材质往往也有部分反射，光线在穿过两种透明介质之间的平面时，部分能量会折射入物体内部，其余的能量会反射出去。

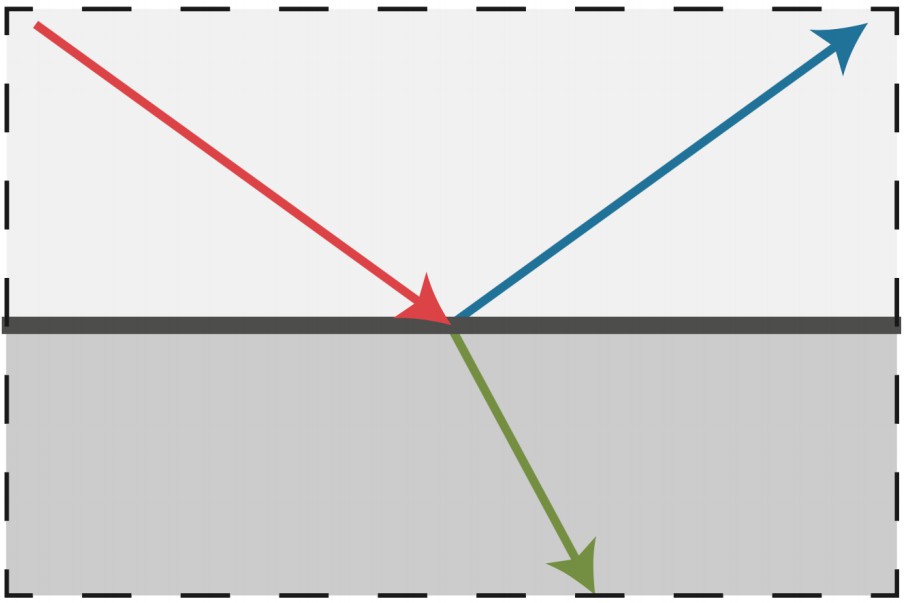
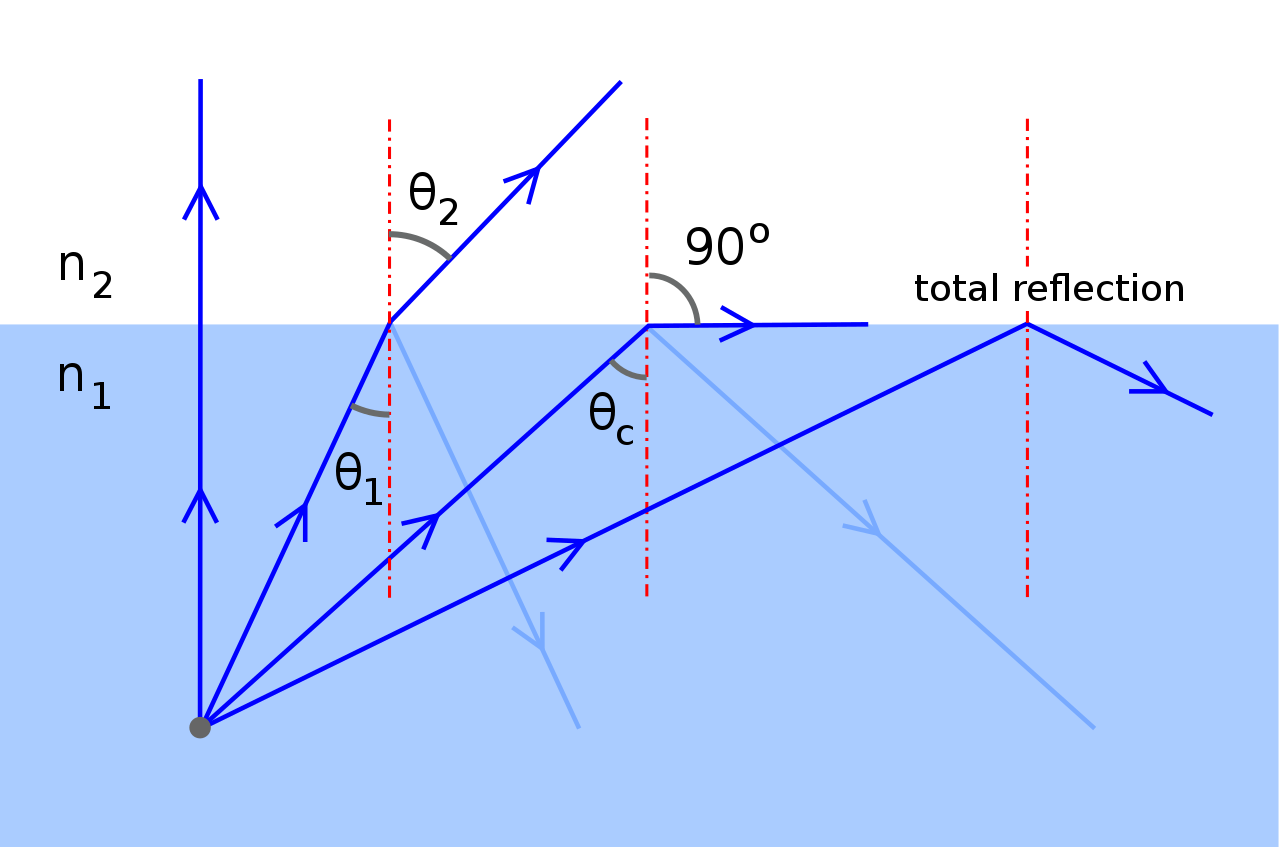
在折射时入射角θ_i与折射角θ_t的关系与平面两侧透明介质的折射率有关，当光线从折射率小的透明物体（例如空气）射入折射率大的透明物体（例如水）中时，折射角会小于入射角，如下图所示。

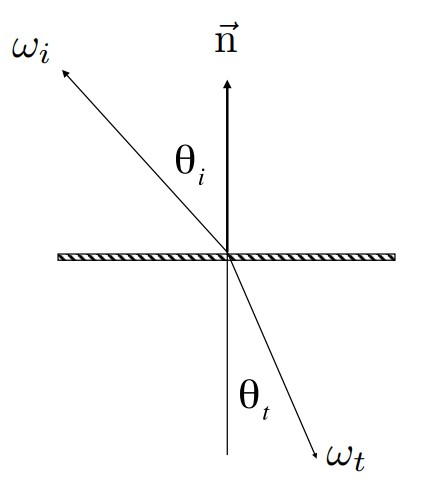
那么如果反过来，光线从折射率大的透明物体进入到折射率小的物体时，同时会发生折射和反射，入射角会小于折射角，那么随着入射角增大，折射角也会增大，折射光线能量减弱，反射光线能量增强，直到折射角达到90度，折射光线完全消失，所有能量都会反射，这就是所谓的全反射现象（Total Internal Reflection），用于通信服务的光纤就是根据全反射原理制成的。

常见物体的折射率如下：

真空	1.0000
空气	1.00029
冰	1.3090
水（20°C）	1.3333
玻璃	1.5~1.6
水晶	1.544～1.553
红宝石、蓝宝石	1.7700
钻石	2.4170

折射方向的计算是由折射定理(Snell’s Law)得来的：

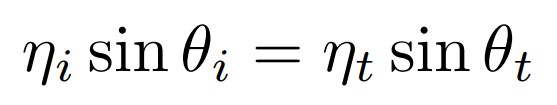
其中ni，nt分别代表平面两边透明介质的折射率，如下图所示上半部分为ni，下半部分为nt：

根据三角函数的关系

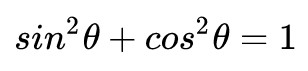
以及前面的折射定理，得到折射角的余弦值cosθt

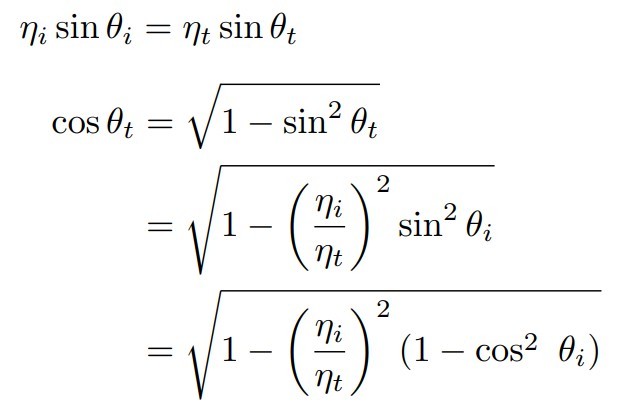
注意，这里是有求平方根操作的，而当根号内小于0时求平方根是无意义的，那么根号内会有小于0的情况吗？

显然，当ni/nt大于1，并且θ_i的比较大时，可能会出现求折射角无意义的情况，也就是前面所说的全反射现象了。

对于折射来说BRDF（Bidirectional Reflectance Distribution Function，双向反射分布函数 ）自然就不适用了，折射适用于BTDF（Bidirectional Transmittance Distribution Function，双向透射分布函数 ），两者可以统称为BSDF（Bidirectional Scattering Distribution Function，双向散射分布函数）。

 

菲涅尔反射（Fresnel Reflection）

入射光线与平面的夹角除了影响折射的效果以外，也影响反射的效果，例如下图

从图中可以看出，桌面的反射效果和视线与桌面的夹角有关，视线越平行桌面，桌面的反射效果越强，书的倒影越清晰；视线越垂直桌面，桌面的反射效果越弱，书的倒影越模糊。

简单来说，就是物体的反射率其实与观察角度有关，对于绝缘体来说观察角度与法线夹角越大，反射的程度就越高，如下图中的红线：

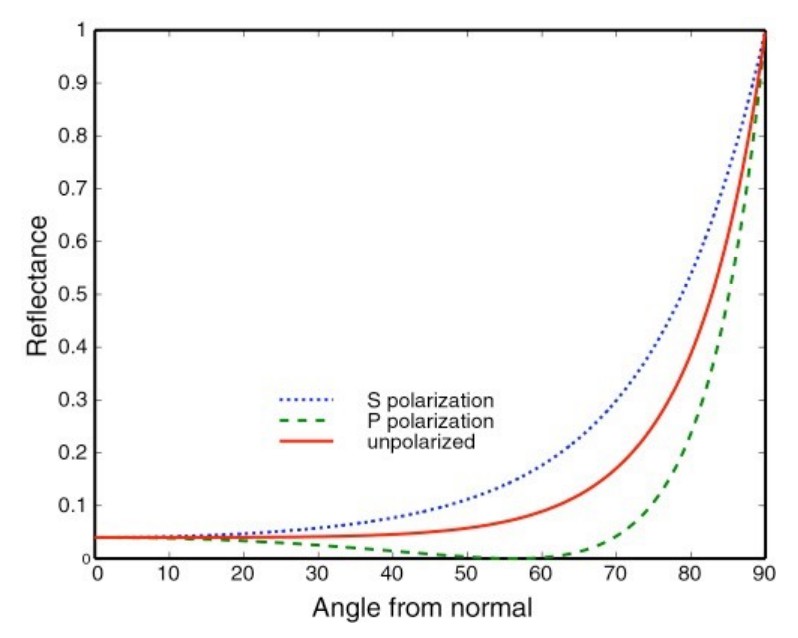
而导体则与绝缘体不同，他的反射率与夹角呈如下关系:

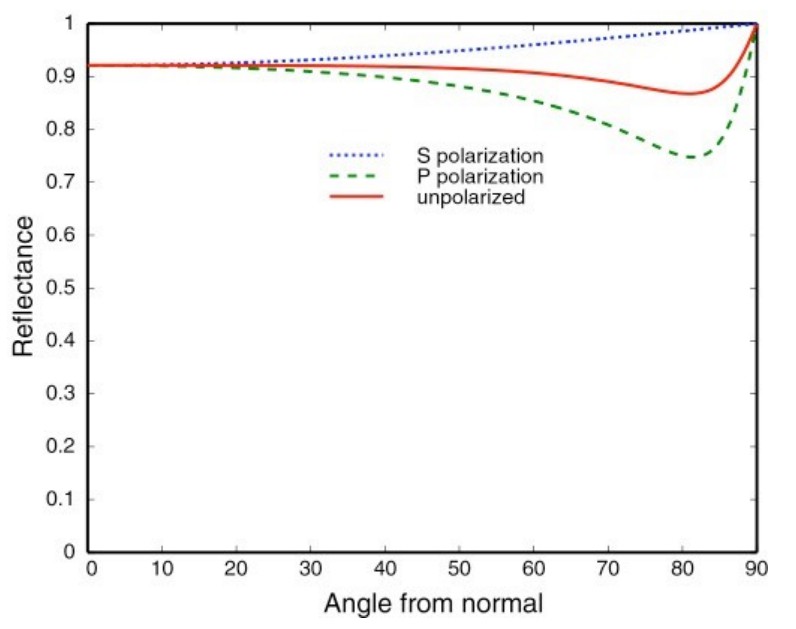
金属的菲涅尔反射现象确实不明显，从哪个视角观察反射效果都比较清晰。

对于任意一个物体的精确反射率的计算公式如下：

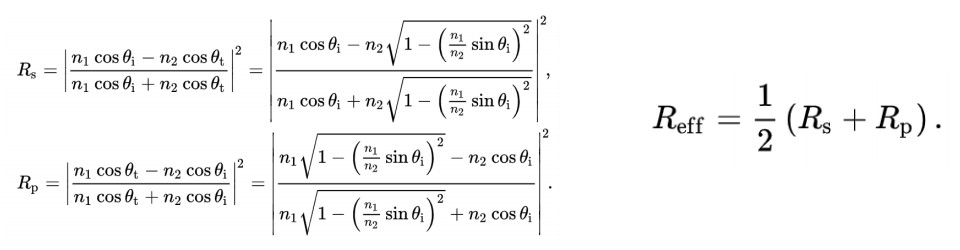
这里考虑了两个极化，然后再求平均，公式的推理过程暂时不必深究，只要知道，物体的反射率和入射角度、入射空间的折射率、物体的折射率有关就可以了，通过该公式就能得出正确的反射率。

对于精确的算法来说，计算量是非常大的，因此有人提出了个简单的算法，大幅降低计算量来得到比较近似的效果，如下：

 

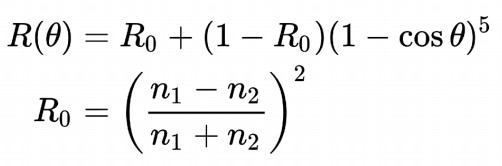
微平面材质（Microfacet Material）

说到微平面材质就不得不提微平面理论(Microfacets Theory)，微平面理论就是从微观的角度去分析，认为任意物体的表面都是由许许多多的更小的镜面所组成，并且每个微小的平面都有自己的法线方向：

当这些微小的镜面的法线方向分布较为集中一致（从数学上看它们的方差较小）的时候，从宏观角度来看，物体的表面会显得比较光滑，镜面反射比较明显；反之，当这些微小镜面的法线方向分布较为杂乱的时候，物体的表面则会显得相对粗糙，漫反射比较明显。如下图所示：

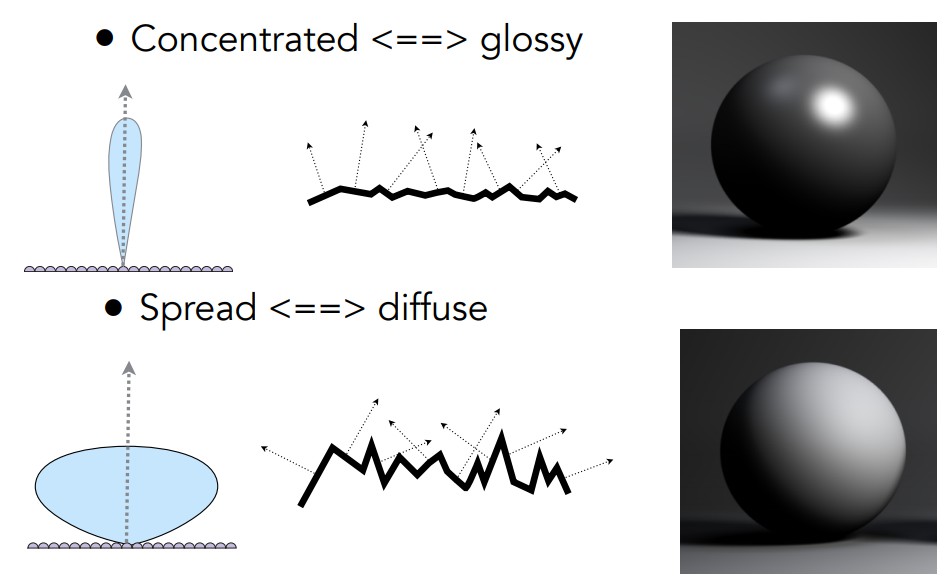
而根据微平面理论和BRDF，也就可以推导出微平面BRDF（Microfacet BRDF）

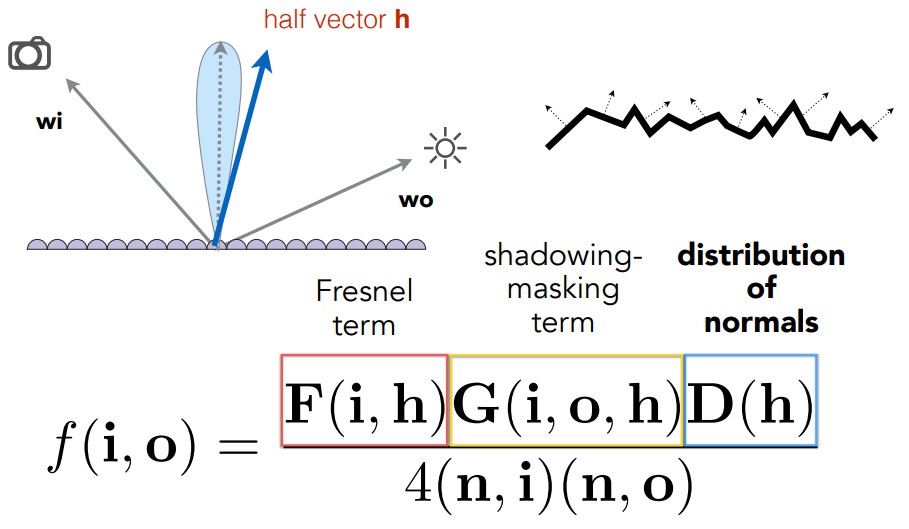
微平面BRDF首先考虑菲涅尔反射F(i, h)，然后考虑法线分布D(h)，这里又用到了半程向量h（入射方向与观察方向的中间向量hDir），只有当微表面的法线方向在半程向量周围一个限定的范围之内时，才能将光反射出去。

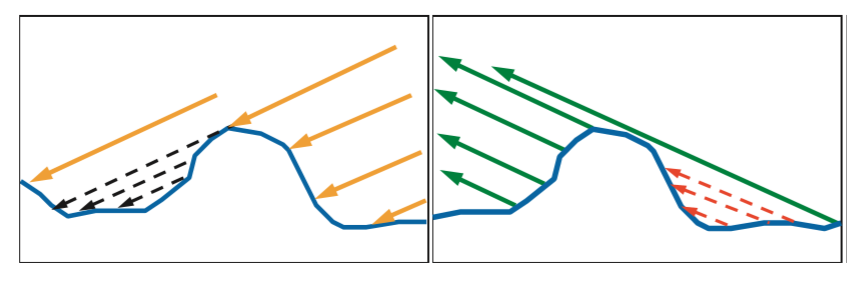
中间那一项G(i, o, h)是考虑微表面之间的光线遮挡，比如当光线接近平行平面的时候，入射光线可能无法照射到一些微平面，这种情况称为Shadowing（如下图左），或者反射光线无法正常到达人眼，称为Masking（如下图右）。

 

各向同性/各向异性材质（Isotropic / Anisotropic Materials）

一些金属表面，往往会进行一些磨砂处理，在表面形成沿一定方向的划痕，也就是微表面存在明确的方向性，从而影响反射的效果，这样的材质就称其为各向异性材质（Anisotropic Materials）；反之微表面不存在方向性或者方向性很微弱的材质就称为各向同性材质（Isotropic Materials）。

各向异性反应在BRDF上就是：

BRDF原来是两个方向的函数θ_i、φ_i是输入方向，θ_r、φ_r是输出方向。如果BRDF满足在方位角上旋转，得到的还是相同的BRDF（沿一个方位角θ或φ的中心旋转，相对位置不变），就称为各向同性；如果相对位置改变，BRDF改变，则称为各向异性。

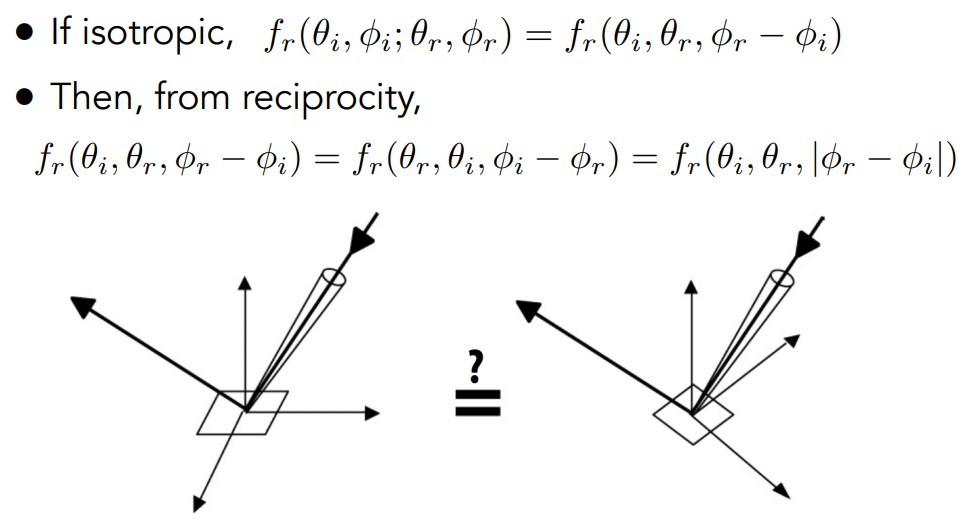
对于各向同性材质，BRDF只和相对的方位角有关，即φr-φi，因此原来四维的BRDF，就可以写成三维的。

所有的BRDF，由于具有可逆性（交换入射方向和出射方向，得到的BRDF的值相同），因此相对方位角不用考虑正负，因此也可以写成方位角之差的绝对值，不用考虑大小或者正负关系。

其他的各向异性材质还有尼龙、天鹅绒等类型：

 

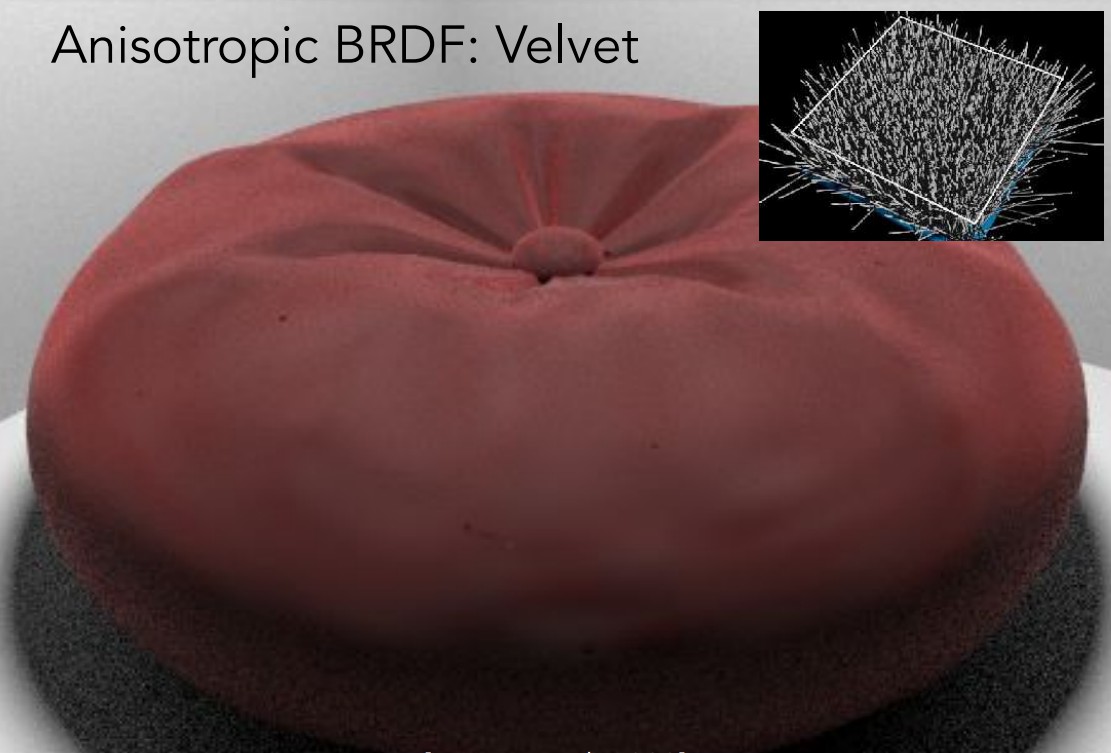
本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记，感谢。

---

所有的战争宣传，
所有的叫嚣、谎言和仇恨，
都来自那些不上战场的人。

——乔治·奥威尔