前言

前文说了着色步骤的基础光照模型，这一篇就说一下几种着色的方法，也就是着色频率。

所谓的着色频率，就是把着色应用在哪些“点”上，主要有三种，面着色，顶点着色，像素着色，下面会一一介绍。

 

面着色Flat Shading

面着色，顾名思义以每一个面作为一个着色单位，一个平面只做一次shading。模型数据大多以很多个三角面进行存储，因此也就记录了每个面的法线向量，利用每个面的法线向量进行一次Blinn-Phong反射光照模型的计算，将该颜色赋予整个面，效果如下：

其中的面法线除了直接从模型信息中读取外，也可以通过三角形的两条边向量做叉乘得到。

Flat Shading 虽然计算很快，只需对每一个面进行一次着色计算，但是效果是很差的，可以很明显的看到一块块三角面的形状。

因此一种改进方法就是对三角形面的每个顶点进行着色，再对三角形面内的颜色插值，即Gouraud Shading。

 

顶点着色Gouraud Shading

Gouraud Shading会对每个三角形的顶点进行一次着色，那么首当其冲的问题就是，现在只有每个面的法线向量，如何得到每个顶点的法线向量呢？

其实很简单，将所有共享这个点的面的法线向量加起来求均值，最后再标准化就得到该顶点的法线向量了。

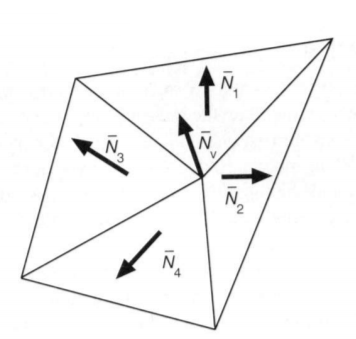
由于不同三角面的面积往往会有较大差别，会导致某个三角面的法线对于该顶点影响更大的情况，因此可以采用加权平均，将该三角面的面积也代入，去求顶点的法线向量。

有了每个三角形的顶点向量之后，自然就可以计算出每个顶点的颜色了，那么对于三角形内部的每一个点再进行插值处理（例如双线性插值），这样就能成功的得到每一个点的颜色了，效果如下：

可以明显看出相对于Flat Shading，Gouraud Shading的效果有着明显的提升，但这样依然还不是最好的做法，因为我们实际上只对每个三角形顶点进行了着色，然后其它的颜色都是通过插值得到，三角面稍大一些就会导致高光等细节被模糊。

那么有没有一种做法可以真正的对每个点用Blinn-Phong模型计算得出颜色呢？没错，那就是Phong Shading了！

 

像素着色Phong Shading

注意，这里说的Phong Shading和Phong光照模型是两个不同的概念，只是发明这两项技术的人是同一个人而已。

Phong Shading的做法其实也是很好理解的，既然要对每个像素点都进行光照计算，那么自然应该要有内部每个点的法线向量才可以。

三角形内部任意点的法线向量可以通过重心坐标算法进行插值得到，该算法下面会具体说明。

三种着色频率在模型的不同细分时对比渲染效果如下：

可以看出每种着色方式各有利弊，在顶点数量较少时，面着色计算速度最快效果最差，像素着色计算速度最慢而效果最好；而在顶点数量非常多时，面着色和顶点着色的效果和像素着色差异不大，计算速度也会变慢，因此需要根据具体场景选择使用。

 

重心坐标算法

先说一下重心坐标（Barycentric Coordinates）的定义。

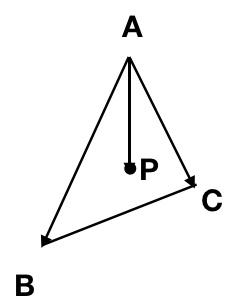
对于三角形ABC内的一点P，根据向量的原理，几个向量AP与AB和AC线性相关，必定可以写成以下形式

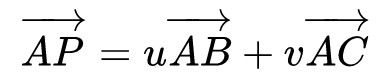
这个式子如果从向量拆成点坐标整理则得到

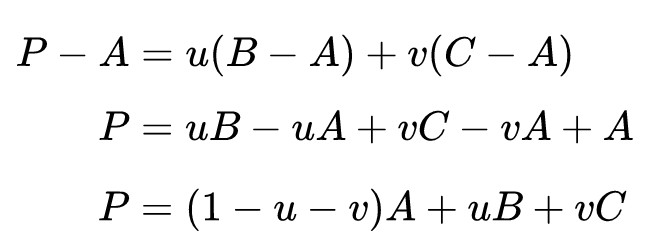
因此三角形的三点坐标A, B, C，该平面内一点P(x,y)可以写成这三点坐标的线性组合形式，即

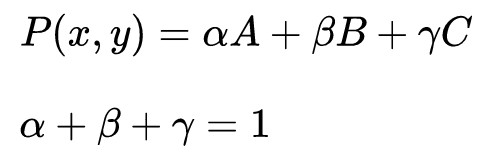
此时α,β,γ称为点P的重心坐标。

进一步变化可得

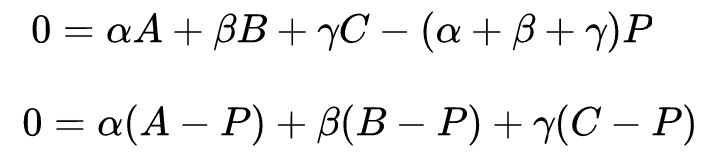
转换成向量就是

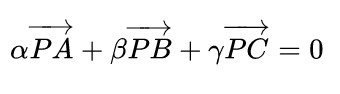
这意味着当在三角形三个顶点ABC处分别悬挂质量为α、β、γ的重物时，P点正好为整个三角形的重心，这就是“重心坐标”名称的由来。

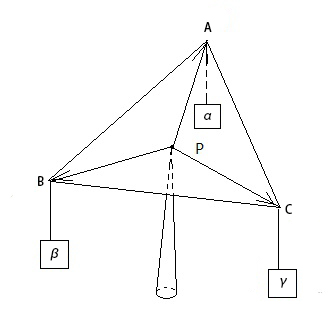
显然当P点的3个重心坐标都是大于0小于1的时候，P点一定在三角形内部；当有一个重心坐标为0时，P点一定在三角形边上；当有两个重心坐标为0时，P点一定在三角形的顶点上。

因此在判断一个点是否在三角形内时，完全可以用重心坐标是否都大于0来代替之前的叉乘(其实二者一定程度上是等价的)。

而反过来如果已知三点坐标A、B、C和所挂重物质量e、d、f，给定三角形内任意一点O的坐标，则可以先求出点O的重心坐标α、β、γ，就能得到O点所受的ABC点的合力F。

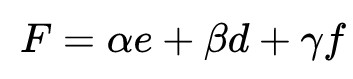
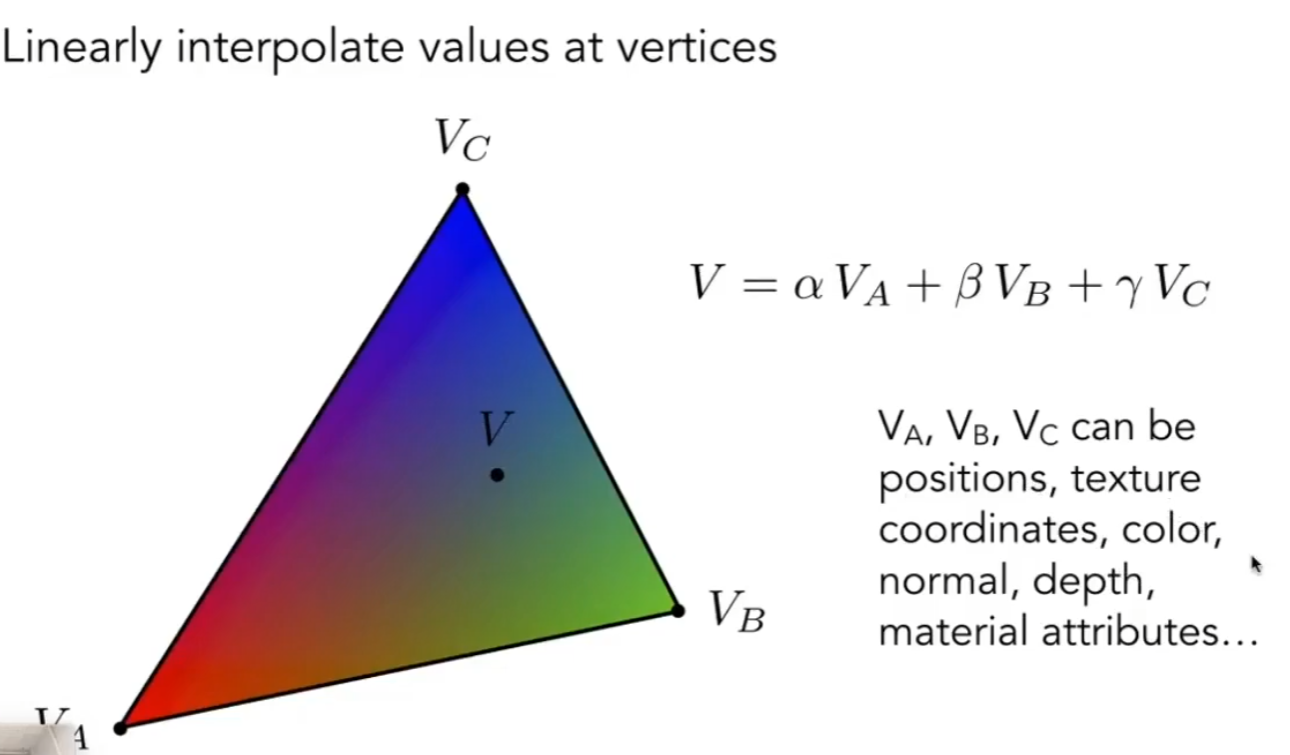
换句话说重心坐标可以用来计算三角形的三个顶点对于内部任意一点的影响能力，因此重心坐标在图形学中最重要的运用便是插值，他可以根据三个顶点A,B,C的属性插值出任意点的属性，无论是位置，UV、颜色，深度，法线向量等等。

那么重心坐标的这三个值如何求解呢？

首先回到最开始的向量处。

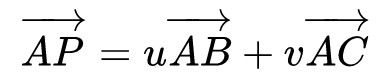
先转换成点坐标

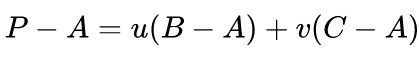
再写成矩阵形式

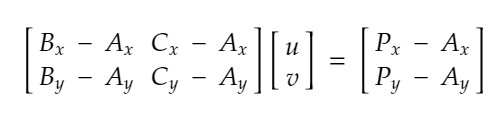
根据矩阵乘法原理，可以转化成两个方程组，就可以得到两个未知数u、v的值，再根据三个重心坐标相加为1就可以得到第三个重心坐标的值。

 

几何面积定义

重心坐标还有一种等价的定义方式，就是通过三角形的面积比。

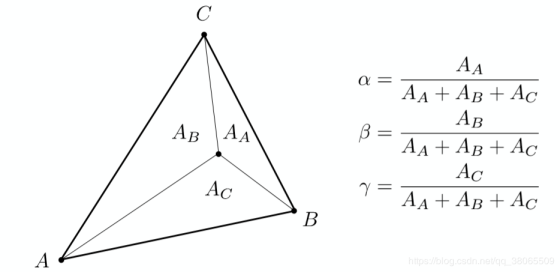
将一点(x,y)与A,B,C三点直接连接，构成三个三角形面积分别为Aa、Ab、Ac，即可直接定义出重心坐标如图中公式所示。

根据这条定义，只需求出各个三角形的面积便可以直接得出重心坐标了。

已知图中4点坐标，那么求出面积自然是很简单的，除了用向量叉乘的方式以外，这里也可以利用行列式的几何意义直接求解，即任意2个2维向量组合成矩阵的行列式的绝对值，为这两条向量所围成平行四边形的面积 。

设任意一点为P(x,y)，则由：

具体的计算就不写了，最终得到的结果应该和上面那种算法的结果一致。

如果将这种几何面积定义扩展，则三维空间的重心坐标就是ABCD四个点构成的四面体中，重心点和三个点构成的四面体占整个四面体的比例，这里就不展开讲了。

 

重心坐标的局限性

三角形在投影变换下不能保证重心坐标不变， 比如从三维中的三角形投影到二维中， 因为投影的三角形会变形， 所以其重心坐标的系数也会改变。

因此对于三维空间中的属性， 插值时应该用三维中的坐标进行插值，假如已经投影到二维空间中了， 那么就需要先逆变换回去再计算重心坐标。

 

本文参考自本文参考自闫令琪老师的《GAMES101-现代计算机图形学入门》和孙晓磊的计算机图形学系列笔记，感谢。

历史不会重复，
但总是押韵。

——马克·吐温